
���� ��1����ȥ������������C1����ͨ���̣����P�ļ����꣬���������P��ֱ�����ꣻ
��2����ֱ��l����б��Ϊ$\frac{2��}{3}$�Ҿ�����P��д���������̴���x2-y2=4�������ɵ�t2+8t+12=0��������|PA|+|PB|��ֵ��
��� �⣺��1������C1�IJ���������$\left\{\begin{array}{l}{x=\sqrt{m}+\frac{1}{\sqrt{m}}}\\{y=\sqrt{m}-\frac{1}{\sqrt{m}}}\end{array}\right.$��mΪ����������ȥm�ɵ�x2-y2=4��
$��=\frac{��}{3}$����=2�����P��ֱ������Ϊ��1��$\sqrt{3}$����
��2��ֱ��l����б��Ϊ$\frac{2��}{3}$�Ҿ�����P����������Ϊ$\left\{\begin{array}{l}{x=1-\frac{1}{2}t}\\{y=\sqrt{3}+\frac{\sqrt{3}}{2}t}\end{array}\right.$��
����x2-y2=4�������ɵ�t2+8t+12=0��
��A��B��Ӧ�IJ����ֱ�Ϊt1��t2����t1+t2=-8��t1t2=12��
��|PA|+|PB|=|t1|+|t2|=|t1+t2|=8
���� ���⿼���˲������̻�Ϊֱ�����귽�̡�ֱ�߲������̵�Ӧ�ã�������������������������������е��⣮


 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m�Φ���m�Φ£�����Φ� | B�� | �����Φ£�m?����n�ͦ£���m��n | ||
| C�� | ��m�ͦ���m��n����n�Φ� | D�� | �����ͦ£�m?����n�ͦ£���m��n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���������� | B�� | ֱ�������� | C�� | ����ֱ�������� | D�� | �ȱ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
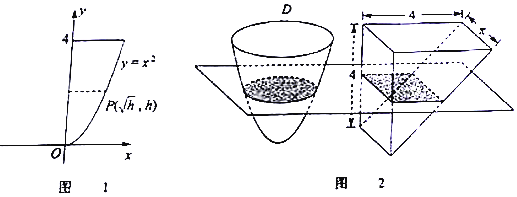
| A�� | $\frac{16��}{3}$ | B�� | 6�� | C�� | 8�� | D�� | 16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����x��cm�� | 60 | 70 | 80 | 90 | 100 | 110 |
| ����y��kg�� | 6 | 8 | 10 | 14 | 15 | 18 |
| ${\widehate^{��1��}}$ | 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| ${\widehate^{��2��}}$ | -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com