
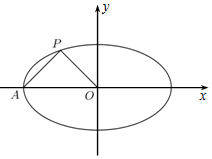
 ����ԲM��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$����ΪA������ΪO������ԲM����$P��-\frac{1}{2}��\frac{1}{2}��$����AP��PO��
����ԲM��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$����ΪA������ΪO������ԲM����$P��-\frac{1}{2}��\frac{1}{2}��$����AP��PO������ ��1������AP��OP����֪kAP•kOP=-1��A������Ϊ��-a��0������a�����b��Ȼ�������Բ���̣�
��2�����AP�ķ���x-y+1=0��ͨ��Q����ԲM�ϵĵ㣬�ʿ���$Q��cos�ȣ�\frac{{\sqrt{3}}}{3}sin�ȣ�$��Ȼ�����������ε����������ֵ���ɣ�
��3��ֱ��AD����Ϊy=k1��x+1��������x2+3y2=1�����D��E���꣬�õ�ֱ��DE�ķ��̣�����ֱ��ϵ�õ��������꣮
����������DE��ֱ��y�ᣬ��xE=-xD��yE=yD����ʱ${k_1}{k_2}=\frac{y_D}{{{x_D}+1}}•\frac{y_E}{{{x_E}+1}}=\frac{{{y_D}^2}}{{1-{x_D}^2}}=\frac{{{y_D}^2}}{{3{y_D}^2}}=\frac{1}{3}$������ì�ܣ���DE����ֱ��y�ᣬ����DE�ķ���Ϊx=ty+s���������x2+3y2=1������Τ�ﶨ�����б�ʹ�ϵ�Ƴ�DE�ķ���Ϊx=ty-2���Ƴ�ֱ��DE�����㣨-2��0����
��� �⣺��1����AP��OP����֪kAP•kOP=-1��
��A������Ϊ��-a��0������$\frac{{\frac{1}{2}}}{{-\frac{1}{2}+a}}•\frac{{\frac{1}{2}}}{{-\frac{1}{2}}}=-1$���ɵ�a=1������2�֣�
��Ϊ��ԲM��P�㣬��$\frac{1}{4}+\frac{1}{{4{b^2}}}=1$���ɵ�${b^2}=\frac{1}{3}$��
������ԲM�ķ���Ϊ${x^2}+\frac{y^2}{{\frac{1}{3}}}=1$�������������������� ����4�֣�
��2��AP�ķ���Ϊ$\frac{y-0}{{\frac{1}{2}-0}}=\frac{x+1}{{-\frac{1}{2}+1}}$����x-y+1=0��
����Q����ԲM�ϵĵ㣬�ʿ���$Q��cos�ȣ�\frac{{\sqrt{3}}}{3}sin�ȣ�$������6�֣�
����${S_{��APQ}}=\frac{1}{2}��\frac{{\sqrt{2}}}{2}��\frac{{|{cos��-\frac{{\sqrt{3}}}{3}sin��+1}|}}{{\sqrt{2}}}$����8�֣�=$\frac{1}{4}|{\frac{{2\sqrt{3}}}{3}cos����+\frac{��}{6}��+1}|$
��$��+\frac{��}{6}=2k�У�k��Z��$����$��=2k��-\frac{��}{6}��k��Z��$ʱ��S��APQȡ���ֵ��
��S��APQ�����ֵΪ$\frac{{\sqrt{3}}}{6}+\frac{1}{4}$�� ����10�֣�
��3��ֱ��AD����Ϊy=k1��x+1��������x2+3y2=1���ɵ�$��3{k_1}^2+1��{x^2}+6{k_1}^2x+3{k_1}^2-1=0$��${x_A}•{x_D}=\frac{{3{k_1}^2-1}}{{3{k_1}^2+1}}$��
��xA=-1����${x_D}=\frac{{1-3{k_1}^2}}{{1+3{k_1}^2}}$��${y_D}={k_1}��\frac{{1-3{k_1}^2}}{{1+3{k_1}^2}}+1��=\frac{{2{k_1}}}{{1+3{k_1}^2}}$������12�֣�
ͬ���ɵ�${x_E}=\frac{{1-3{k_2}^2}}{{1+3{k_2}^2}}$��${y_E}=\frac{{2{k_2}}}{{1+3{k_2}^2}}$����k1k2=1��k1��k2���ɵ�${k_2}=\frac{1}{k_1}$��k1�١�1��
����${x_E}=\frac{{{k_1}^2-3}}{{{k_1}^2+3}}$��${y_E}=\frac{{2{k_1}}}{{{k_1}^2+3}}$��${k_{DE}}=\frac{{{y_E}-{y_D}}}{{{x_E}-{x_D}}}=\frac{{\frac{{2{k_1}}}{{{k_1}^2+3}}-\frac{{2{k_1}}}{{1+3{k_1}^2}}}}{{\frac{{{k_1}^2-3}}{{{k_1}^2+3}}-\frac{{1-3{k_1}^2}}{{1+3{k_1}^2}}}}=\frac{{2{k_1}}}{{3��{k_1}^2+1��}}$��
ֱ��DE�ķ���Ϊ$y-\frac{{2{k_1}}}{{1+3{k_1}^2}}=\frac{{2{k_1}}}{{3��{k_1}^2+1��}}��x-\frac{{1-3{k_1}^2}}{{1+3{k_1}^2}}��$������14�֣�
��y=0���ɵ�$x=\frac{{1-3{k_1}^2}}{{1+3{k_1}^2}}-\frac{{3��{k_1}^2+1��}}{{1+3{k_1}^2}}=-2$��
��ֱ��DE�����㣨-2��0���� ����16�֣�
����������DE��ֱ��y�ᣬ��xE=-xD��yE=yD��
��ʱ${k_1}{k_2}=\frac{y_D}{{{x_D}+1}}•\frac{y_E}{{{x_E}+1}}=\frac{{{y_D}^2}}{{1-{x_D}^2}}=\frac{{{y_D}^2}}{{3{y_D}^2}}=\frac{1}{3}$������ì�ܣ�
��DE����ֱ��y�ᣬ����DE�ķ���Ϊx=ty+s���������x2+3y2=1��
�ɵã�t2+3��y2+2tsy+s2-1=0���ɵ�${y_D}+{y_E}=\frac{-2ts}{{{t^2}+3}}��{y_D}•{y_E}=\frac{{{s^2}-1}}{{{t^2}+3}}$������12�֣�
��${k_1}{k_2}=\frac{y_D}{{{x_D}+1}}•\frac{y_E}{{{x_E}+1}}=\frac{{{y_D}{y_E}}}{{��t{y_D}+s+1����t{y_E}+s+1��}}=1$��
�ɵ�$��{t^2}-1��{y_D}{y_E}+t��s+1����{y_D}+{y_E}��+{��s+1��^2}=0$������14�֣�
��$��{t^2}-1��\frac{{{s^2}-1}}{{{t^2}+3}}+t��s+1��\frac{-2ts}{{{t^2}+3}}+{��s+1��^2}=0$��
�ɵ�s=-2��-1����DE����A�㣬��s��-1����s=-2��
����DE�ķ���Ϊx=ty-2����ֱ��DE�����㣨-2��0���� ����16�֣�
���� ���⿼����Բ���̵���ֱ������Բ��λ�ù�ϵ������ת��˼���Լ�����������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com