
分析 (1)根据求和公式列方程求出q,代入通项公式即可;
(2)对a进行讨论,判断{bn}的单调性和首项的符号,从而得出Tn的最值.
解答 解:(1)∵${S_3}=4{S_2}-\frac{5}{16}$,∵q≠1,∴$\frac{{{a_1}(1-{q^3})}}{1-q}=4×\frac{{{a_1}(1-{q^2})}}{1-q}-\frac{5}{16}$.
整理得q2-3q+2=0,解得q=2或q=1(舍去).
∴${a_n}={a_1}×{q^{n-1}}={2^{n-5}}$.
(2)bn=logaan=(n-5)loga2.
∴数列{bn}是以loga2为公差,以-4loga2为首项的等差数列,
∴Tn=-4nloga2+$\frac{n(n-1)}{2}$loga2=$\frac{{n}^{2}-9n}{2}$•loga2.
1)当a>1时,有loga2>0,数列{bn}是以loga2为公差,以-4loga2为首项的等差数列,
∴{bn}是递增数列,∴Tn没有最大值.
由bn≤0,得n≤5.所以(Tn)min=T4=T5=-10loga2.
2)当0<a<1时,有loga2<0,数列{bn}是以loga2为公差的等差数列,
∴{bn}是首项为正的递减等差数列.∴Tn没有最小值.
令bn≥0,得n≤5,(Tn)max=T4=T5=-10loga2.
点评 本题考查了等比数列,等差数列的性质,数列求和,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{n}$ | B. | $\frac{n}{n+1}$ | C. | $\frac{1}{n+1}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
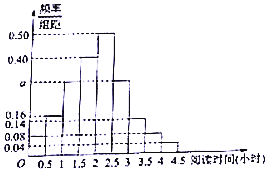 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成样本的频率分布直方图如图所示.
某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成样本的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
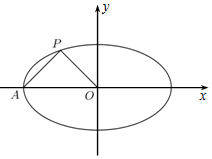 设椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A、中心为O,若椭圆M过点$P(-\frac{1}{2},\frac{1}{2})$,且AP⊥PO.
设椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A、中心为O,若椭圆M过点$P(-\frac{1}{2},\frac{1}{2})$,且AP⊥PO.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com