练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．某所学校计划招聘男教师x名，女教师y名，x和y须满足约束条件$\left\{\begin{array}{l}2x-y≥5\\ x-y≤2\\ x＜5.\end{array}\right.$则该校招聘的教师人数最多是7名．

    分析 由题意由于某所学校计划招聘男教师x名，女教师y名，且x和y须满足约束条件$\left\{\begin{array}{l}2x-y≥5\\ x-y≤2\\ x＜5.\end{array}\right.$，又不等式组画出可行域，又要求该校招聘的教师人数最多令z=x+y，则题意求解在可行域内使得z取得最大．

    解答 解：由于某所学校计划招聘男教师x名，女教师y名，且x和y须满足约束条件$\left\{\begin{array}{l}2x-y≥5\\ x-y≤2\\ x＜5.\end{array}\right.$，画出可行域为：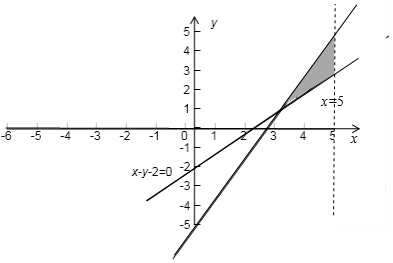

    对于需要求该校招聘的教师人数最多，
    令z=x+y?y=-x+z 则题意转化为，在可行域内任意去x，y且为整数使得目标函数代表的斜率为定值-1，
    截距最大时的直线为过$\left\{\begin{array}{l}{x=4}\\{2x-y-5=0}\end{array}\right.$⇒（4，3）时使得目标函数取得最大值为：z=7．
    故答案为：7．

    点评 此题考查了线性规划的应用，还考查了学生的数形结合的求解问题的思想．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．袋中有5个除了颜色外完全相同的小球，包括2个红球，2个黑球和1个白球，从中随机摸出2个球，则这2个球颜色不同的概率为$\frac{4}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知集合A={x|lnx＞0}，B={x|2x＜3}，则A∩B=（1，log23）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系，已知直线l的参数方程为$\left\{\begin{array}{l}x=t\\ y=t+2\end{array}\right.$，（t为参数），曲线C的普通方程为x2-4x+y2-2y=0，点P的极坐标为（2$\sqrt{2}$，$\frac{7π}{4}$）．
    （1）求直线l的普通方程和曲线C的极坐标方程；
    （2）若将直线l向右平移2个单位得到直线l′，设l′与C相交于A，B两点，求△PAB的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．对某地区儿童的身高与体重的一组数据，我们用两种模型①y=bx+a，②y=cedx拟合，得到回归方程分别为${\widehaty^{（1）}}=0.24x-8.81$，${\widehaty^{（2）}}=1.70{e^{0.022x}}$，作残差分析，如表：
    身高x（cm）60708090100110
    体重y（kg）6810141518
    ${\widehate^{（1）}}$0.410.011.21-0.190.41
    ${\widehate^{（2）}}$-0.360.070.121.69-0.34-1.12
    （Ⅰ）求表中空格内的值；
    （Ⅱ）根据残差比较模型①，②的拟合效果，决定选择哪个模型；
    （Ⅲ）残差大于1kg的样本点被认为是异常数据，应剔除，剔除后对（Ⅱ）所选择的模型重新建立回归方程．
    （结果保留到小数点后两位）
    附：对于一组数据（x1，y1），（x2，y2），…（xn，yn），其回归直线y=bx+a的斜率和截距的最小二乘法估计分别为$\widehatb=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}$，$\widehata=\overline y-\widehatb\overline x$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

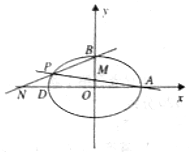    4．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{1}{2}$，A（a，0），b（0，b），D（-a，0），△ABD的面积为$2\sqrt{3}$．
    （1）求椭圆C的方程；
    （2）如图，设P（x0，y0）是椭圆C在第二象限的部分上的一点，且直线PA与y轴交于点M，直线PB与 x轴交于点N，求四边形ABNM的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．在平面直角坐标系xOy中，设圆x2+y2-4x=0的圆心为Q．
    （1）求过点P（0，-4）且与圆Q相切的直线的方程；
    （2）若过点P（0，-4）且斜率为k的直线与圆Q相交于不同的两点A，B，以OA、OB为邻边做平行四边形OACB，问是否存在常数k，使得?OACB为矩形？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知抛物线Γ：y2=2px（p＞0）的焦点为F．若过点F且斜率为1的直线与抛物线Γ相交于M，N两点，又△MON的面积为${S_{△MON}}=\frac{{\sqrt{2}}}{2}$．
    （1）求抛物线Γ的方程；
    （2）若点P是抛物线Γ上的动点，点B，C在y轴上，圆（x-1）2+y2=1内切于△PBC，求△PBC的面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知F点为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一个焦点，以点F为圆心的圆于C的渐近线相切，且与C交于A，B两点，若AF⊥x轴，则C的离心率为$\sqrt{2}$．

    查看答案和解析>>

    同步练习册答案