
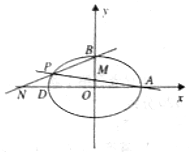
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{1}{2}$,A(a,0),b(0,b),D(-a,0),△ABD的面积为$2\sqrt{3}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{1}{2}$,A(a,0),b(0,b),D(-a,0),△ABD的面积为$2\sqrt{3}$.分析 (1)根据椭圆的离心率公式及三角形的面积公式,即可求得a和b的值,即可求得椭圆方程;
(2)求得直线PA的方程,求得丨BM丨,同理求得丨AN丨,由${S_{四边形ABNM}}=\frac{1}{2}|{AN}|•|{BM}|$,代入即可求得四边形ABNM的面积.
解答 解:(1)由题意得$\left\{\begin{array}{l}\frac{c}{a}=\frac{1}{2}\\ \frac{1}{2}({2a})b=2\sqrt{3}\\{a^2}={b^2}+{c^2}\end{array}\right.$,解得a=2,$b=\sqrt{3}$.
∴椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)由(1)知,A(2,0),$B({0,\sqrt{3}})$,由题意可得${S_{四边形ABNM}}=\frac{1}{2}|{AN}|•|{BM}|$,
因为P(x0,y0),-2<x0<0,$0<{y_0}<\sqrt{3}$,$3x_0^2+4y_0^2=12$.
∴直线PA的方程为$y=\frac{y_0}{{{x_0}-2}}(x-2)$
令x=0,得${y_M}=-\frac{{2{y_0}}}{{{x_0}-2}}$.从而$|{BM}|=|{\sqrt{3}-{y_M}}|$=$|{\sqrt{3}+\frac{{2{y_0}}}{{{x_0}-2}}}|$.
直线PB的方程为$y=\frac{{{y_0}-\sqrt{3}}}{x_0}x+\sqrt{3}$.
令y=0,得${x_N}=-\frac{{\sqrt{3}{x_0}}}{{{y_0}-\sqrt{3}}}$.从而|AN|=|2-xN|=$|{2+\frac{{\sqrt{3}{x_0}}}{{{y_0}-\sqrt{3}}}}|$.
∴|AN|•|BM|=$|{2+\frac{{\sqrt{3}{x_0}}}{{{y_0}-\sqrt{3}}}}|•|{\sqrt{3}+\frac{{2{y_0}}}{{{x_0}-2}}}|$,
=$|{\frac{{3x_0^2+4y_0^2+4\sqrt{3}{x_0}{y_0}-12{x_0}-8\sqrt{3}{y_0}+12}}{{{x_0}{y_0}-\sqrt{3}{x_0}-2{y_0}+2\sqrt{3}}}}|$,
=$|{\frac{{4\sqrt{3}{x_0}{y_0}-12{x_0}-8\sqrt{3}{y_0}+24}}{{{x_0}{y_0}-\sqrt{3}{x_0}-2{y_0}+2\sqrt{3}}}}|$,
=$4\sqrt{3}$.
∴${S_{四边形ABNM}}=\frac{1}{2}|{AN}|•|{BM}|$=$2\sqrt{3}$,
四边形ABNM的面积2$\sqrt{3}$.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤3} | B. | {x|1<x<2} | C. | {x|0≤x≤1} | D. | {x|2<x≤3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com