
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() .则下列结论正确的是( ).
.则下列结论正确的是( ).
A.当![]() 时,
时,![]()
B.函数![]() 有五个零点
有五个零点
C.若关于![]() 的方程
的方程![]() 有解,则实数
有解,则实数![]() 的取值范围是
的取值范围是![]()
D.对![]() ,
,![]() 恒成立
恒成立
【答案】AD
【解析】
根据函数![]() 是奇函数,求出
是奇函数,求出![]() 时的解析式,可判断A;利用导数求出函数
时的解析式,可判断A;利用导数求出函数![]() 在
在![]() 上的单调区间及极值,再结合
上的单调区间及极值,再结合![]() 是奇函数,可作出函数
是奇函数,可作出函数![]() 在
在![]() 上的大致图象,从而可逐项判断B、C、D.
上的大致图象,从而可逐项判断B、C、D.
设![]() ,则
,则![]() ,所以
,所以![]() ,
,
又函数![]() 是定义在
是定义在![]() 上的奇函数,所以
上的奇函数,所以![]() ,
,
所以![]() ,即
,即![]()
故A正确.
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故当![]() 时,函数
时,函数![]() 取得极小值
取得极小值![]() ,
,
当![]() 时,
时,![]() ,又
,又![]() ,故函数
,故函数![]() 在
在![]() 仅有一个零点
仅有一个零点![]() .
.
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 没有零点,
没有零点,
所以函数![]() 在
在![]() 上仅有一个零点,函数
上仅有一个零点,函数![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,
故函数![]() 在
在![]() 上仅有一个零点
上仅有一个零点![]() ,又
,又![]() ,
,
故函数![]() 是定义在
是定义在![]() 上有3个零点.
上有3个零点.
故B错误.
作出函数![]() 的大致图象,由图可知
的大致图象,由图可知

若关于![]() 的方程
的方程![]() 有解,则实数
有解,则实数![]() 的取值范围是
的取值范围是![]() .
.
故C错误.
由图可知,对![]() ,
,![]()
故D正确.
故选:AD.


科目:高中数学 来源: 题型:
【题目】不重合的两条直线![]() ,
,![]() 和不重合的两个平面
和不重合的两个平面![]() ,
,![]() ,下面的几个命题:①若
,下面的几个命题:①若![]() ,且
,且![]() ,则
,则![]() ;②若
;②若![]() ,
,![]() 与平面
与平面![]() 成等角,则
成等角,则![]() ;③若
;③若![]() ,
,![]() ,且
,且![]() ,则
,则![]() ;④若
;④若![]() ,
,![]() ,则
,则![]() ;⑤若
;⑤若![]() ,
,![]() 异面,且
异面,且![]() ,
,![]() 均与平面
均与平面![]() 和
和![]() 平行,则
平行,则![]() .在这5个命题中,真命题的个数是( )
.在这5个命题中,真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知AB为圆O的直径,且![]() ,点D为线段AO的中点,点C为圆O上的一点,且
,点D为线段AO的中点,点C为圆O上的一点,且![]() ,
,![]() 平面ABC,
平面ABC,![]() .
.

(1)求证:![]() 平面PAB.
平面PAB.
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
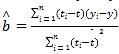 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注,受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为![]() ,女性观众认为《流浪地球》好看的概率为
,女性观众认为《流浪地球》好看的概率为![]() .某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
.某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
(1)求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率;
(2)设![]() 表示这4名观众中认为《流浪地球》好看的人数,求
表示这4名观众中认为《流浪地球》好看的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为1.
截得的线段长为1.
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 是椭圆
是椭圆![]() 上除长轴端点外的任一点,连接
上除长轴端点外的任一点,连接![]() ,
,![]() ,设
,设![]() 的角平分线
的角平分线![]() 交
交![]() 的长轴于点
的长轴于点![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() ,使得
,使得![]() 与椭圆
与椭圆![]() 有且只有一个公共点,设直线
有且只有一个公共点,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,若
,若![]() ,证明
,证明![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在直角梯形ABCD中,AB//CD,AB⊥BC,AB=3BE=3![]() ,CD=2
,CD=2![]() ,AD=2.将△ADE沿DE折起,使平面ADE⊥平面BCDE.
,AD=2.将△ADE沿DE折起,使平面ADE⊥平面BCDE.
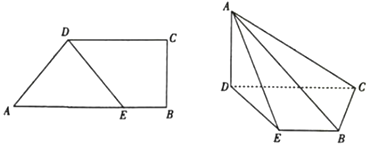
(1)证明:BC⊥平面ACD;
(2)求直线AE与平面ABC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com