
分析 (1)化圆的方程为标准方程,求出圆心坐标,解出圆心关于直线l1:y=2x+1的对称点,即可得到圆C的圆心坐标,求得圆C的标准方程;
(2)分直线l的斜率存在和不存在两种情况讨论,当直线斜率不存在时,直接求出直线方程,与圆的方程联立求出A,B的坐标,已知$\overrightarrow{OA}•\overrightarrow{OB}=0$即可;当直线的斜率存在时,设出直线方程,与圆的方程联立,化为关于x的一元二次方程,利用根与系数的关系求得A,B的横坐标的和与积,代入向量垂直的坐标运算求得k,则直线方程可求.
解答 解:(1)圆C1化为标准式为(x+3)2+y2=9,
设圆C1的圆心C1(-3,0)关于直线l1:y=2x+1的对称点为C(a,b),
则${k}_{C{C}_{1}}•{k}_{{l}_{1}}=-1$,且CC1的中点$M({\frac{a-3}{2},\frac{b}{2}})$在直线l1:y=2x+1上,
∴有$\left\{\begin{array}{l}{\frac{b}{a+3}×2=-1}\\{({a-3})-\frac{b}{2}+1=0}\end{array}$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}$,
∴圆C的方程为(x-1)2+(y+2)2=9;
(2)要使OA⊥OB,必须使$\overrightarrow{OA}•\overrightarrow{OB}=0$,即:x1x2+y1y2=0.
①当直线l的斜率不存在时,可得直线l的方程为x=-1,与圆C:(x-1)2+(y+2)2=9交于两点$A({-1,\sqrt{5}-2})$,$B({-1,-\sqrt{5}-2})$.
∵$\overrightarrow{OA}•\overrightarrow{OB}=({-1})({-1})+({\sqrt{5}-2})({-\sqrt{5}-2})=0$,∴OA⊥OB,
∴当直线l的斜率不存在时,直线l:x=-1满足条件.
②当直线l的斜率存在时,可设直线l的方程为y=k(x+1).
设A(x1,y1),B(x2,y2)
由$\left\{\begin{array}{l}{(x-1)^{2}+(y+2)^{2}=9}\\{y=k(x+1)}\end{array}\right.$得:(1+k2)x2+(2k2+4k-2)x+k2+4k-4=0.
${x_1}+{x_2}=-\frac{{2{k^2}+4k-2}}{{1+{k^2}}}$,${x_1}{x_2}=\frac{{{k^2}+4k-4}}{{1+{k^2}}}$,
由于点(-1,0)在圆C内部,∴△>0恒成立.
要使OA⊥OB,必须使$\overrightarrow{OA}•\overrightarrow{OB}=0$,即x1x2+y1y2=0,
也就是:${x}_{1}{x}_{2}+{k}^{2}({x}_{1}+1)({x}_{2}+1)=0$,
即${k}^{2}({x}_{1}+{x}_{2})+({k}^{2}+1){x}_{1}{x}_{2}+{k}^{2}=0$,
∴$-{k}^{2}•\frac{2{k}^{2}+4k-2}{1+{k}^{2}}+({k}^{2}+1)•\frac{{k}^{2}+4k-4}{1+{k}^{2}}+{k}^{2}=0$
整理得:4k-4=0,解得:k=1,
∴直线l的方程为y=x+1.
故存在直线x=-1和y=x+1,使得OA⊥OB.
点评 本题考查直线与圆位置关系的应用,体现了“设而不求”的解题思想方法,在处理平面解析几何时,往往先设出直线方程,但要注意直线的斜率是否存在,是中档题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | [-$\sqrt{3}$,-$\sqrt{2}$)∪($\sqrt{2}$,$\sqrt{3}$) | C. | [-3,-1)∪(1,3] | D. | [-$\sqrt{3}$,-$\sqrt{2}$)∪($\sqrt{2}$,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
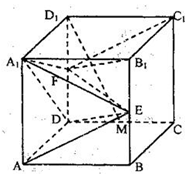 在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1的中点,M为棱DC的中点.
在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1的中点,M为棱DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②③ | C. | ②③④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,且|F1F2|=4$\sqrt{3}$,M($\sqrt{3}$,-$\frac{\sqrt{13}}{2}$)是椭圆上一点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,且|F1F2|=4$\sqrt{3}$,M($\sqrt{3}$,-$\frac{\sqrt{13}}{2}$)是椭圆上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 组别 | 第一组 | 第二组 | 第三组 | 第四组 |
| 相关系数r | -0.98 | 0.80 | 0.50 | -0.25 |
| A. | 第一组 | B. | 第二组 | C. | 第三组 | D. | 第四组 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com