
已知函数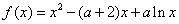 ,其中
,其中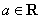 .
.
(Ⅰ)若曲线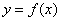 在点
在点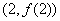 处的切线的斜率为
处的切线的斜率为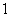 ,求
,求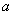 的值;
的值;
(Ⅱ)求函数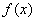 的单调区间.
的单调区间.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
抛物线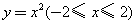 绕
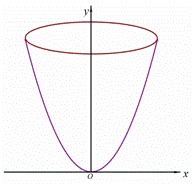
绕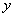 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是
(A)1 (B)8 (C)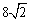 (D)
(D)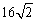
查看答案和解析>>
科目:高中数学 来源: 题型:
在一次抽奖活动中,有a、b、c、d、e、f 共6人获得抽奖的机会。抽奖规则如下:主办方先从6人中随机抽取两人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖。
(Ⅰ)求a能获一等奖的概率;
(Ⅱ)若a、b已获一等奖,求c能获奖的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
设 是由
是由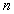 个有序实数构成的一个数组,记作:
个有序实数构成的一个数组,记作: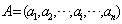 .其中
.其中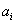
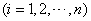 称为数组
称为数组 的“元”,
的“元”,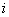 称为
称为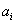 的下标. 如果数组
的下标. 如果数组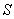 中的每个“元”都是来自 数组
中的每个“元”都是来自 数组 中不同下标的“元”,则称
中不同下标的“元”,则称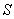 为
为 的子数组. 定义两个数组
的子数组. 定义两个数组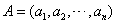 ,
,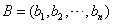 的关系数为
的关系数为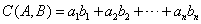 .
.
(Ⅰ)若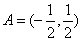 ,
,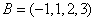 ,设
,设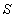 是
是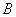 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求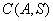 的最大值;
的最大值;
(Ⅱ)若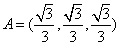 ,
,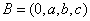 ,且
,且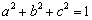 ,
,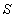 为
为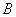 的含有三个“元”的子数组,求
的含有三个“元”的子数组,求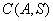 的最大值;
的最大值;
(Ⅲ)若数组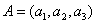 中的“元”满足
中的“元”满足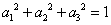 .设数组
.设数组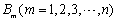 含有四个“元”
含有四个“元”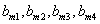 ,且
,且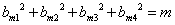 ,求
,求 与
与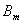 的所有含有三个“元”的子数组的关系数
的所有含有三个“元”的子数组的关系数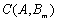
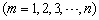 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com