
分析 求出平面ABC的法向量为$\overrightarrow{n}$=(1,1,1),利用方向向量为$\overrightarrow j=(0,0,1)$的直线与平面ABC所成角的余弦值=sin<$\overrightarrow{n}$,$\overrightarrow{j}$>,即可得出结论
解答 解:设平面ABC的法向量为$\overrightarrow{n}$=(a,b,c),则$\left\{\begin{array}{l}{a-3b+2c=0}\\{-2a-b+3c=0}\end{array}\right.$,
取a=1,可得平面ABC的法向量为$\overrightarrow{n}$=(1,1,1),
∴cos<$\overrightarrow{n}$,$\overrightarrow{j}$>=$\frac{\sqrt{3}}{3}$,
∴方向向量为$\overrightarrow j=(0,0,1)$的直线与平面ABC所成角θ的余弦值cosθ=sin<$\overrightarrow{n}$,$\overrightarrow{j}$>=$\sqrt{1-\frac{1}{3}}$=$\frac{\sqrt{6}}{3}$.
点评 本题考查线面角,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [0,4] | C. | {1,2,3,4} | D. | {0,1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{10}{3}$ | D. | -$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q是假命题 | B. | p∨(¬q)是假命题 | C. | p∧q是真命题 | D. | p∧(¬q)是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈R,使得x2>2x”的否定是“?x∈R,使得x2≤2x” | |
| B. | “若a∈(0,1),则关于x的不等式ax2+2ax+1>0的解集为R”的逆命题为真 | |
| C. | “若a、b不都是偶数,则a+b不是偶数”的否命题为假 | |
| D. | “已知a,b∈R若a+b≠3,则a≠2或b≠1”的逆否命题为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
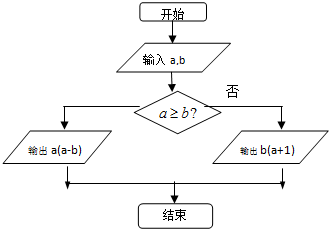
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x∈R,则x2≥0”的否命题为:“若x∈R,则x2<0” | |
| B. | “sinα=1”是“α=$\frac{π}{2}$”的充分不必要条件 | |
| C. | 若命题p为真命题,命题q为假命题,则命题“p且q”为真命题 | |
| D. | 命题“对任意x∈R,都有2x>0”的否定是“存在x0∈R,都有2x0≤0” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com