
 的图象为曲线
的图象为曲线 , 函数
, 函数 的图象为直线
的图象为直线 .
. 时, 求
时, 求 的最大值;
的最大值; 与曲线
与曲线 的交点的横坐标分别为
的交点的横坐标分别为 , 且
, 且 ,
,  .
. 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源:不详 题型:解答题
 是直线
是直线 上三点,向量
上三点,向量 满足:
满足: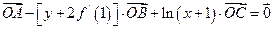 ,且函数
,且函数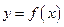 定义域内可导。
定义域内可导。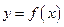 的解析式;
的解析式;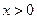 ,证明:
,证明: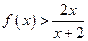 ;
;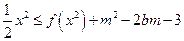 对
对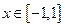 及
及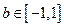 都恒成立,求实数
都恒成立,求实数 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (x∈R),经验证:当c=1,2,3时,不等式对一切实数x都成立。试问:当c取任何正数时,不等式对任何实数x是否都成立?若能成立,请给出证明;若不成立,请求出c的取值范围,使不等式对任何实数x都能成立。
(x∈R),经验证:当c=1,2,3时,不等式对一切实数x都成立。试问:当c取任何正数时,不等式对任何实数x是否都成立?若能成立,请给出证明;若不成立,请求出c的取值范围,使不等式对任何实数x都能成立。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (1)若
(1)若
 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围; (2)若
的取值范围; (2)若 是
是 的极值点,求
的极值点,求 在
在 上的最大值;(3)在(2)的条件下,是否存在实数
上的最大值;(3)在(2)的条件下,是否存在实数 ,使得函数
,使得函数 的图像与函数
的图像与函数 的图象恰有3个交点?若存在,请求出实数
的图象恰有3个交点?若存在,请求出实数 的取值范围;若不存在,试说明理由。
的取值范围;若不存在,试说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
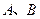 两地相距
两地相距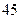 千米,
千米, 骑车人与客车分别从
骑车人与客车分别从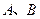 两地出发,往返于
两地出发,往返于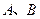 两地之间.下图中,折线表示某骑车人离开
两地之间.下图中,折线表示某骑车人离开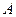 地的距离
地的距离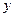 与时间
与时间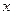 的函数关系.客车
的函数关系.客车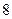 点从
点从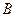 地出发,以
地出发,以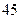 千米/时的速度匀速行驶.(乘客上、下车停车时间忽略不计)
千米/时的速度匀速行驶.(乘客上、下车停车时间忽略不计) 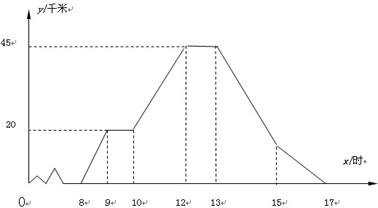
 图的基础上,直接回答:
图的基础上,直接回答: 骑车人共休息几次?骑车人总共骑行多少千米?骑车人与客车总共相遇几次?
骑车人共休息几次?骑车人总共骑行多少千米?骑车人与客车总共相遇几次? 出演算过程).
出演算过程).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com