
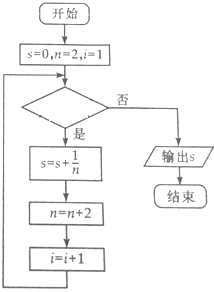
分析 模拟执行程序框图,依次写出每次循环得到的s,n的值,当i=11时,不满足条件,退出循环,从而可得判断框中的条件.
解答 解:模拟执行程序框图,可得
当i=1时,满足条件,s=$\frac{1}{2}$,n=4
当i=2时,满足条件,s=$\frac{1}{2}$$+\frac{1}{4}$,n=6
…
当i=10时,满足条件,s=$\frac{1}{2}$$+\frac{1}{4}$+…+$\frac{1}{20}$,n=22
由题意可得,当i=11时,不满足条件,退出循环,输出s=$\frac{1}{2}$$+\frac{1}{4}$+…+$\frac{1}{20}$的值,
所以判断框中的条件是“i≤10?”.
点评 本题考查求程序框图中循环结构中的判断框中的条件,模拟程序的运行是解题的常用方法,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
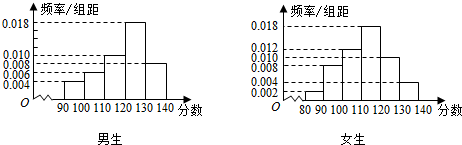
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | |||
| 女生 | |||
| 总计 |
| K0 | 2.072 | 2.076 | 3.814 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|-6≤a<2} | B. | {a|-4≤a<2}∪{-5}∪{-6} | C. | {a|-5≤a<2}∪{-6} | D. | {a|-4≤a<2}∪{-$\frac{14}{3}$}∪{-6} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
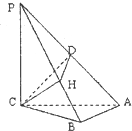 三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )
三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com