
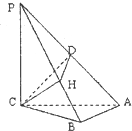
 三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )
三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
分析 先证出△CHD是直角三角形,再利用基本不等式得出CH=DH=$\sqrt{2}$时△CDH的面积最大;
再利用三角形的等积法求出BC的值.
解答 解:三棱锥P-ABC中,PC⊥面ABC,AB?平面ABC,∴PC⊥AB;
又AB⊥BC,BC∩PC=C,
∴AB⊥平面PBC;
又CH?平面PBC,
∴AB⊥CH,
又CH⊥PB,
PB∩AB=B,
∴CH⊥平面PAB,
又DH?平面PAB,
∴CH⊥DH;
又△PAC是等腰直角三角形,且PA=4,D是PA的中点,
∴CD=$\frac{1}{2}$PA=2,
设CH=a,DH=b,
则a2+b2=CD2=4,
∴4=a2+b2≥2ab,
即$\frac{1}{2}$ab≤1,
当且仅当a=b=$\sqrt{2}$时,“=”成立,此时△CDH的面积最大;
在Rt△PBC,设BC=x,
则PB=$\sqrt{{PC}^{2}{+BC}^{2}}$=$\sqrt{{(2\sqrt{2})}^{2}{+x}^{2}}$=$\sqrt{8{+x}^{2}}$,
∴$\frac{1}{2}$PC•BC=$\frac{1}{2}$PB•CH,
即2$\sqrt{2}$•x=$\sqrt{8{+x}^{2}}$•$\sqrt{2}$;
解得x=$\frac{2\sqrt{6}}{3}$,
∴CB的长是$\frac{2\sqrt{6}}{3}$.
故选:D.
点评 本题考查了空间几何体的平行与垂直关系的应用问题,也考查了面积公式的应用问题,考查了利用基本不等式求最值的问题,是综合性题目.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 5 | C. | 8 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com