
分析 运用角的等价变化得到sin($\frac{π}{3}$-α)=$\frac{3}{5}$=sin($\frac{π}{2}-\frac{π}{6}$-α)=cos($\frac{π}{6}+α$),运用倍角公式求值.
解答 解:因为sin($\frac{π}{3}$-α)=$\frac{3}{5}$=sin($\frac{π}{2}-\frac{π}{6}$-α)=cos($\frac{π}{6}+α$),
则sin($\frac{π}{6}$-2α)=sin($\frac{π}{2}-\frac{π}{3}$-2α)=cos($\frac{π}{3}+2α$)=cos2($\frac{π}{6}+α$)=2cos2($\frac{π}{6}+α$)-1=-$\frac{7}{25}$;
故答案为:-$\frac{7}{25}$.
点评 本题考查了三角函数式的化简求值;灵活对角进行等价变化,运用倍角公式求值是关键.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
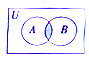
| A. | {1,2,3,4,5} | B. | {3,4,5,6,7} | C. | {1,2,3,4,5,6,7} | D. | {3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分又不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $0<\frac{b}{a}≤\frac{3}{2}$ | B. | $\frac{b}{a}≥\frac{3}{2}$ | C. | $0<\frac{b}{a}≤\frac{{\sqrt{5}}}{2}$ | D. | $\frac{b}{a}≥\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $2+\sqrt{3}$ | C. | $2+\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,4} | B. | {0,1,6} | C. | {0,2,4} | D. | {0,4,16} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,半圆O的半径为1,A为直径延长线上一点,OA=2,B为半圆上任意一点,以AB为一边做等边三角形ABC,设∠AOB=θ.
如图,半圆O的半径为1,A为直径延长线上一点,OA=2,B为半圆上任意一点,以AB为一边做等边三角形ABC,设∠AOB=θ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com