
分析 (1)根据双曲线的实轴长为2$\sqrt{3}$,一个焦点的坐标为$(-\sqrt{5},0)$,求出a,b的值即可求出双曲线的方程.
(2)利用直线和双曲线相交的弦长公式进行求解即可.
解答 解:(1)∵实轴长为2$\sqrt{3}$,一个焦点的坐标为$(-\sqrt{5},0)$,
∴$2a=2\sqrt{3}$,得$a=\sqrt{3}$,$c=\sqrt{5}$,
∴b2=c2-a2=2,
∴双曲线C 的方程为$\frac{x^2}{3}-\frac{y^2}{2}=1$.
(2)设直线l 的方程为y=2x+m,A(x1,y1),B(x2,y2),
由$\left\{{\begin{array}{l}{y=2x+m}\\{\frac{x^2}{3}-\frac{y^2}{2}=1}\end{array}}\right.$,得10x2+12mx+3(m2+2)=0,
∴△=24(m2-10)>0,得$|m|>\sqrt{10}$,
∴弦长$|AB|=\frac{{\sqrt{5}\sqrt{24({m^2}-10)}}}{10}=4$,解得$m=±\frac{{\sqrt{210}}}{3}$,
∴直线l 的方程为$y=2x+\frac{{\sqrt{210}}}{3}$ 或$y=2x-\frac{{\sqrt{210}}}{3}$.
点评 本题主要考查双曲线的方程以及直线和双曲线的位置关系的应用,利用设而不求的思想是解决本题的关键.考查学生的运算能力.


科目:高中数学 来源: 题型:填空题
| x | 2 | 3 | 4 | 5 |
| y | 2.2 | 3.8 | 4.5 | 5.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A. | 10.5 | B. | 5.15 | C. | 5.25 | D. | 5.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $\sqrt{15}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
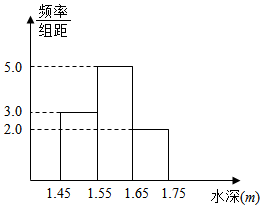 为研究某灌溉渠道水的流速y(m/s)和水深x(cm)之间的关系,现抽测了100次,统计出其流速的平均值为1.92,水深的频率直方图如图.已知流速对水深的线性回归方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+0.012.若水深的平均值用每组数据的中值(同一数据用该区间中点值作代表)来估计,则估计$\stackrel{∧}{b}$约为( )
为研究某灌溉渠道水的流速y(m/s)和水深x(cm)之间的关系,现抽测了100次,统计出其流速的平均值为1.92,水深的频率直方图如图.已知流速对水深的线性回归方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+0.012.若水深的平均值用每组数据的中值(同一数据用该区间中点值作代表)来估计,则估计$\stackrel{∧}{b}$约为( )| A. | 0.3 | B. | 0.6 | C. | 0.9 | D. | 1.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com