已知函数
.
（1）请用“五点法”画出函数
在长度为一个周期的闭区间上的简图（先在所给的表格中填上所需的数值，再画图）；
| | | | | | |
| | | | | | |
| | | | | | |
的单调递增区间；
时，求函数的最大值和最小值及相应的
的值. （1）过程见解析;（2）
;（3）当x=0时,函数取得最小值
；当x=
p时,函数取得最大值1.
解析试题分析：（1）画三角函数图象的方法是五点法,具体步骤是1.列表,标出一个周期内与x轴的交点和最大值点与最小值点;2.描点,将列出的5个点画在平面直角坐标系中;3.连线,用平滑的曲线连接5点;由题,列表如下,描点连线; （2）三角函数sinx在[-
p,p]上递增,在[p,
p]上递减,由题,令
,可解得,故函数f(x)在递增;（3）由x的范围可以得到2x-
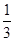p的范围,再由（2）中函数的增减性可以求得最大值和最小值.
试题解析：（1）令
，则
．填表：
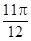
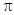
（2）令,
解得,
∴函数
的单调增区间为
.
（3）∵
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目：高中数学 来源： 题型：解答题
设函数f(x)=msinx+cosx(x∈R)的图象经过点(
,1).
(1)求f(x)的解析式,并求函数的最小正周期.
(2)若f(α+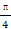
)=
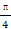且α∈(0,),求f(2α-)的值.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
设向量a＝(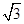
sin x，sin x)，b＝(cos x，sin x)，x∈
.
(1)若|a|＝|b|，求x的值；
(2)设函数f(x)＝a·b，求f(x)的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝
sin ωx－sin2
＋
(ω>0)的最小正周期为π.
(1)求ω的值及函数f(x)的单调递增区间；
(2)当x∈
时，求函数f(x)的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
的周期为
.
（1）若
，求它的振幅、初相；
（2）在给定的平面直角坐标系中作出该函数在
的图像；
（3）当时，根据实数
的不同取值，讨论函数
的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，
分别是
的三个内角
，
，
所对的边，且
．
，
，求
.
的最小正周期和图像的对称轴方程；
上的值域.
，
，函数
。
的值域和函数的单调递增区间; 
,且
时,求
的值.
，
，且
。
)取最大值时，判断三角形ABC的形状。