Question

2．函数f（x）=3x²+e^x-2（x＜0）与g（x）=3x²+ln（x+t）图象上存在关于y轴对称的点，则t的取值范围是（　　）

• A． （-∞，$\frac{1}{e}$）
• B． （-∞，e）
• C． （-e，$\frac{1}{e}$）
• D． （-$\frac{1}{e}$，e）

Answer 1

分析 若函数f（x）=3x²+e^x-2（x＜0）与g（x）=3x²+ln（x+t）的图象上存在关于y轴对称的点，则函数f（x）=3x²+e^x-2（x＜0）关于y对称后的图象与g（x）=3x²+ln（x+t）的图象有交点，进而可得实数t的取值范围．

解答 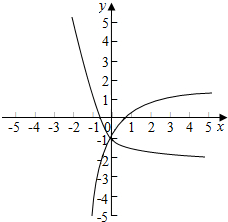解：若函数f（x）=3x²+e^x-2（x＜0）与g（x）=3x²+ln（x+t）的图象上存在关于y轴对称的点，
则函数f（x）=3x²+e^x-2（x＜0）关于y对称后的图象与g（x）=3x²+ln（x+t）的图象有交点，
即2x²+e^-x=2x²+ln（x+t）+2有正根，
即e^-x=ln（x+t）+2有正根，
即e^-x-2=ln（x+t）有正根，
即函数y=e^-x-2和y=ln（x+t）的图象在y轴右侧有交点，
如下图所示：
由lnt=-1得：t=$\frac{1}{e}$得：满足条件的实数m的取值范围是（-∞，$\frac{1}{e}$），
故选：A．

点评 本题主要考察函数图象的对称变换，函数交点个数及位置的判定，属于中档题．