
分析 将函数y=$\sqrt{3}$sin2x-cos2x化解为y=Asin(ωx+φ)的形式,再利用函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:函数y=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$).
由函数$y=2sin(2x+\frac{π}{6})$=2sin[2(x+$\frac{π}{3}$)]的图象向右平移$\frac{π}{6}$,可得2sin[2(x+$\frac{π}{3}$-$\frac{π}{6}$)]=2sin(2x-$\frac{π}{6}$)
故答案为$\frac{π}{6}$.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{e}$) | B. | (-∞,e) | C. | (-e,$\frac{1}{e}$) | D. | (-$\frac{1}{e}$,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | 2 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
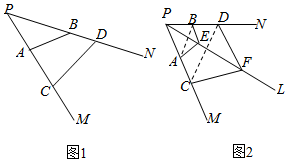 平面上,点A、C为射线PM上的两点,点B、D为射线PN上的两点,则有$\frac{{{S_{△PAB}}}}{{{S_{△PCD}}}}=\frac{PA•PB}{PC•PD}$(其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有$\frac{{{V_{P-ABE}}}}{{{V_{P-CDF}}}}$=$\frac{PA•PB•PE}{PC•PD•PF}$(其中VP-ABE、VP-CDF分别为四面体P-ABE、P-CDF的体积).
平面上,点A、C为射线PM上的两点,点B、D为射线PN上的两点,则有$\frac{{{S_{△PAB}}}}{{{S_{△PCD}}}}=\frac{PA•PB}{PC•PD}$(其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有$\frac{{{V_{P-ABE}}}}{{{V_{P-CDF}}}}$=$\frac{PA•PB•PE}{PC•PD•PF}$(其中VP-ABE、VP-CDF分别为四面体P-ABE、P-CDF的体积).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|3≤x<7}, | B. | {x|2<x<10} | C. | {x|x≤2或x≥10} | D. | {x|x<3或x≥7} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com