
分析 (Ⅰ)求出函数的导数,计算判别式△,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)问题转化为$\frac{2}{{1-{x^2}}}(1nx-a\frac{x-1}{x+1})<0$,即$\frac{2}{{1-{x^2}}}f(x)<0$,结合函数的单调性求出a的范围即可.
解答 解:(Ⅰ)定义域是(0,+∞),
$f'(x)=\frac{1}{x}-\frac{2a}{{{{(x+1)}^2}}}$=$\frac{{{x^2}+2(1-a)x+1}}{{x{{(x+1)}^2}}}$.
令g(x)=x2+2(1-a)x+1.
当△=4(1-a)2-4≤0,
即0≤a≤2时,g(x)≥0恒成立,即f'(x)≥0,
所以f(x)的单调增区间为(0,+∞);
当△=4(1-a)2-4>0时,即a<0或a>2时,方程g(x)=0有两个不等的实根,
${x_1}=a-1-\sqrt{{{(a-1)}^2}-1}$,${x_2}=a-1+\sqrt{{{(a-1)}^2}-1}$.
若a<0,由x1+x2=2(a-1)<0,x1x2=1>0得,x1<0,x2<0,
所以g(x)>0在(0,+∞)成立,
即f'(x)>0,所以f(x)的单调增区间为(0,+∞);
若a>2,由x1+x2=2(a-1)>0,x1x2=1>0得,x1>0,x2>0,
由g(x)>0得x的范围是(0,x1),(x2,+∞),由g(x)<0得x的范围(x1,x2),
即f(x)的单调递增区间为(0,x1),(x2,+∞),f(x)的单调递减区间为(x1,x2).
综上所述,当a>2时,f(x)的单调递增区间为$(0,a-1-\sqrt{{{(a-1)}^2}-1})$,$(a-1+\sqrt{{{(a-1)}^2}-1},+∞)$,
f(x)的单调递减区间为$(a-1-\sqrt{{{(a-1)}^2}-1},a-1+\sqrt{{{(a-1)}^2}-1})$;
当a≤2时,f(x)的单调递增区间为(0,+∞),无递减区间.
(Ⅱ)由$\frac{(x+1)1nx+2a}{{{{(x+1)}^2}}}<\frac{1nx}{x-1}$,得$\frac{(x+1)1nx+2a}{{{{(x+1)}^2}}}-\frac{1nx}{x-1}<0$,
即$\frac{-21nx}{{{x^2}-1}}+\frac{2a(x-1)}{{{{(x+1)}^2}(x-1)}}<0$,即$\frac{2}{{1-{x^2}}}(1nx-a\frac{x-1}{x+1})<0$,即$\frac{2}{{1-{x^2}}}f(x)<0$.
由(Ⅰ)可知当a≤2时,f(x)的单调递增区间为(0,+∞),又f(1)=0,
所以当x∈(0,1)时,f(x)<0,当x∈(1,+∞)时,f(x)>0;
又当x∈(0,1)时,$\frac{2}{{1-{x^2}}}>0$,当x∈(1,+∞)时,$\frac{2}{{1-{x^2}}}<0$;
所以$\frac{2}{{1-{x^2}}}f(x)<0$,即原不等式成立.
由(Ⅰ)可知当a>2时,f(x)在(0,x1),(x2,+∞)单调递增,在(x1,x2)单调递减,
且x1x2=1,得x1<1<x2,f(x2)<f(1)=0,
而$\frac{2}{1-x_2^2}<0$,所以$\frac{2}{1-x_2^2}f({x_2})>0$与条件矛盾.
综上所述,a的取值范围是(-∞,2].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
 某大型超市拟对店庆当天购物满288元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.
某大型超市拟对店庆当天购物满288元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )
如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )| A. |  | B. |  | C. | 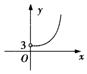 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x≤0,x$+\frac{4}{x}$≤4 | B. | ¬p:?x≤0,x$+\frac{4}{x}$≤4 | C. | ¬p:?x>0,x$+\frac{4}{x}$≤4 | D. | ¬p:?x>0,x$+\frac{4}{x}$=4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com