
| A. | 甲合适 | B. | 乙合适 | ||
| C. | 油价先高后低甲合适 | D. | 油价先低后高甲合适 |
分析 设司机甲每次加油x,司机乙每次加油化费为y;两次加油的单价分别为a,b;从而可得司机甲两次加油的均价为$\frac{a+b}{2}$;司机乙两次加油的均价为$\frac{2ab}{a+b}$;作差比较大小即可.
解答 解:设司机甲每次加油x,司机乙每次加油化费为y;
两次加油的单价分别为a,b;
则司机甲两次加油的均价为$\frac{ax+bx}{2x}$=$\frac{a+b}{2}$;
司机乙两次加油的均价为$\frac{2y}{\frac{y}{a}+\frac{y}{b}}$=$\frac{2ab}{a+b}$;
且$\frac{a+b}{2}$-$\frac{2ab}{a+b}$=$\frac{(a-b)^{2}}{2(a+b)}$≥0,
又∵a≠b,
∴$\frac{a+b}{2}$-$\frac{2ab}{a+b}$>0,
即$\frac{a+b}{2}$>$\frac{2ab}{a+b}$,
故这两次加油的均价,司机乙的较低,
故乙更合适,
故选B.
点评 本题考查了函数在实际问题中的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | 3 | C. | $\frac{7}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC.
如图,在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,且AD=4DC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
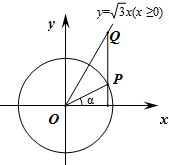 如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9.6元 | B. | 12元 | C. | 15.6元 | D. | 21.6元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | c>b>a | C. | a>b>c | D. | b>c>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com