
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AD=2.
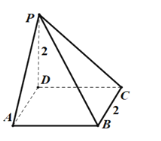
(1)求该四棱锥P-ABCD的表面积和体积;
(2)求该四棱锥P-ABCD内切球的表面积.
【答案】(1) S=8+4![]() ,,V=
,,V=![]() (2) (24-16
(2) (24-16![]() )π.
)π.
【解析】
(1) 四个侧面都是直角三角形,进而求出边长,即可求得侧面积,底面是正方形,二者相加即可求出表面积,PD⊥平面ABCD,故四棱锥的高为![]() ,再由棱锥的体积公式求出体积;
,再由棱锥的体积公式求出体积;
(2) 设内切球的半径为r,球心为O,根据等体积法求出内切球的半径,则由![]() 即可求得半径,进而求出内切球的表面积.
即可求得半径,进而求出内切球的表面积.
(1) 解:(1)由已知底面ABCD为正方形,PD⊥平面ABCD,
![]() ,得PD⊥AD,PD⊥AB,AD⊥AB.
,得PD⊥AD,PD⊥AB,AD⊥AB.
又![]() ,∴AB⊥平面PAD,∴PA⊥AB,∴PA
,∴AB⊥平面PAD,∴PA⊥AB,∴PA![]() PB
PB![]()
∴![]()
![]()
同理![]()
![]()
![]()
∴![]()
![]() .
.
S=8+4![]() ,,V=
,,V=![]()
(2)设内切球的半径为r,球心为O,
则球心O到平面PAB,平面PAD,平面PCB,平面PCD,平面ABCD的距离均为r,
由![]() 可得
可得
![]()
∴![]()
∴![]() .
.
∴r![]() ,S=(24-16
,S=(24-16![]() )π.
)π.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]()
![]() ,又数列
,又数列![]() 满足:
满足:![]() .
.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若数列![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若数列![]() 的各项皆为正数,
的各项皆为正数,![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,问:是否存在整数
项和,问:是否存在整数![]() ,使得数列
,使得数列![]() 是单调递减数列?若存在,求出整数
是单调递减数列?若存在,求出整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率是
的离心率是![]() ,斜率不为0的直线
,斜率不为0的直线![]() :
:![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .
.
(1)若![]() 、
、![]() 分别是
分别是![]() 的左、右焦点,当
的左、右焦点,当![]() 经过
经过![]() 且
且![]() 时,求
时,求![]() 的值;
的值;
(2)试探究,是否存在点![]() ,使得
,使得![]() ?若存在,请写出满足条件的
?若存在,请写出满足条件的![]() 、
、![]() 的关系式;若不存在,说明理由.
的关系式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】至![]() 年底,我国发明专利申请量已经连续
年底,我国发明专利申请量已经连续![]() 年位居世界首位,下表是我国
年位居世界首位,下表是我国![]() 年至
年至![]() 年发明专利申请量以及相关数据.
年发明专利申请量以及相关数据.
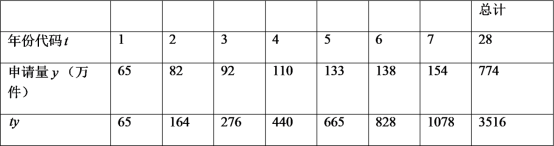
注:年份代码![]() ~
~![]() 分别表示
分别表示![]() ~
~![]() .
.
(1)可以看出申请量每年都在增加,请问这几年中哪一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到
的回归直线方程(精确到![]() ),并预测我国发明专利申请量突破
),并预测我国发明专利申请量突破![]() 万件的年份.
万件的年份.
参考公式:回归直线的斜率和截距的最小二乘法估计分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】峰谷电是目前在城市居民当中开展的一种电价类别.它是将一天24小时划分成两个时间段,把8:00—22:00共14小时称为峰段,执行峰电价,即电价上调;22:00—次日8:00共10个小时称为谷段,执行谷电价,即电价下调.为了进一步了解民众对峰谷电价的使用情况,从某市一小区随机抽取了50 户住户进行夏季用电情况调查,各户月平均用电量以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:度)分组的频率分布直方图如下图:
(单位:度)分组的频率分布直方图如下图:

若将小区月平均用电量不低于700度的住户称为“大用户”,月平均用电量低于700度的住户称为“一般用户”.其中,使用峰谷电价的户数如下表:
月平均用电量(度) |
|
|
|
|
|
|
使用峰谷电价的户数 | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估计所抽取的 50户的月均用电量的众数和平均数(同一组中的数据用该组区间的中点值作代表);
(2)(![]() )将“一般用户”和“大用户”的户数填入下面
)将“一般用户”和“大用户”的户数填入下面![]() 的列联表:
的列联表:
一般用户 | 大用户 | |
使用峰谷电价的用户 | ||
不使用峰谷电价的用户 |
(![]() )根据(
)根据(![]() )中的列联表,能否有
)中的列联表,能否有![]() 的把握认为 “用电量的高低”与“使用峰谷电价”有关?
的把握认为 “用电量的高低”与“使用峰谷电价”有关?
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附:![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
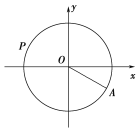
【题目】水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为R的水车,一个水斗从点A(3![]() ,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<
,-3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时60秒.经过t秒后,水斗旋转到P点,设P的坐标为(x,y),其纵坐标满足y=f(t)=Rsin(ωt+φ)(t≥0,ω>0,|φ|<![]() ).则下列叙述错误的是( )
).则下列叙述错误的是( )
A.R=6,ω=![]() ,φ=-
,φ=-![]()
B.当t∈[35,55]时,点P到x轴的距离的最大值为6
C.当t∈[10,25]时,函数y=f(t)单调递减
D.当t=20时,|PA|=6![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 、
、![]() ,
,![]() ,点
,点![]() 在椭圆上,
在椭圆上,![]() 为原点.
为原点.
⑴若![]() ,
,![]() ,求椭圆的离心率;
,求椭圆的离心率;
⑵若椭圆的右顶点为![]() ,短轴长为2,且满足
,短轴长为2,且满足![]() 为椭圆的离心率).
为椭圆的离心率).
①求椭圆的方程;
②设直线![]() :
:![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点,若
两点,若![]() 的面积为1,求实数
的面积为1,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com