
| A. | 若?服从正态分布N(1,2),且P(?>2)=0.1,则P(0<?<2)=0.2 | |
| B. | 命题:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
分析 A,?服从正态分布N(1,2),其正态曲线关于直线x=1对称,由P(?>2)=0.1得P(0<?<2)=0.8,;
B,命题:“?x>1,x2>1”的否定是“?x>1,x2≤1”,只否定结论;
C,直线ax+y+2=0与ax-y+4=0垂直时⇒a•a+1×(-1)=0⇒a=±1,把a=±1代入直线方程验证垂直;
D,”或的否定是“且“.
解答 解:对于A,?服从正态分布N(1,2),其正态曲线关于直线x=1对称,由P(?>2)=0.1得P(0<?<2)=0.8,故错;
对于B,命题:“?x>1,x2>1”的否定是“?x>1,x2≤1”,只否定结论,故错;
对于C,直线ax+y+2=0与ax-y+4=0垂直时⇒a•a+1×(-1)=0⇒a=±1,把a=±1代入直线方程验证垂直,故正确;
对于D,“若xy=0,则x=0或y=0”的逆否命题为“若x≠0且y≠0,则xy≠0“,”或的否定是“且“,故错.
故选:C.
点评 本题考查了命题真假判定,涉及到了大量的基础知识,属于基础题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
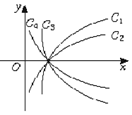 图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )
图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )| A. | $\frac{4}{3}$,$\sqrt{3}$,$\frac{3}{5}$,$\frac{1}{10}$ | B. | $\sqrt{3}$,$\frac{4}{3}$,$\frac{1}{10}$,$\frac{3}{5}$ | C. | $\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$ | D. | $\frac{4}{3}$,$\sqrt{3}$,$\frac{1}{10}$,$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{e^2}+1}}{2}$ | B. | $\frac{{{e^2}-3}}{2}$ | C. | $\frac{{{e^2}+3}}{2}$ | D. | $\frac{{{e^2}-5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提、小前提及推理形式都错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com