
分析 (1)由题意求得c,把P的坐标代入椭圆方程,结合隐含条件求得a2,b2的值,则椭圆方程可求;
(2)设切点坐标为$(\frac{{{y}_{0}}^{2}}{4},{y}_{0})$(y0>0),写出直线l的方程,与椭圆方程联立,利用根与系数的关系求出AB的中点坐标,得到AB的垂直平分线方程,求出N的坐标,进一步得到MN的斜率,然后利用基本不等式求直线MN斜率的最小值.
解答 解:(1)∵点$P(1,\frac{3}{2})$与椭圆右焦点的连线垂直于x轴,
∴c=1,将P点坐标代入椭圆方程可得$\frac{1}{{a}^{2}}+\frac{9}{4{b}^{2}}=1$,
又a2-b2=1,联立可解得a2=4,b2=3,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)设切点坐标为$(\frac{{{y}_{0}}^{2}}{4},{y}_{0})$(y0>0),则l:$y-{y}_{0}=\frac{2}{{y}_{0}}(x-\frac{{{y}_{0}}^{2}}{4})$.
整理,得l:$y=\frac{2}{{y}_{0}}x+\frac{{y}_{0}}{2}$.
∴M($-\frac{{{y}_{0}}^{2}}{4},0$),设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=\frac{2}{{y}_{0}}x+\frac{{y}_{0}}{2}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,可得$(3+\frac{16}{{{y}_{0}}^{2}}){x}^{2}+8x+{{y}_{0}}^{2}-12=0$,
△=$64-4(3+\frac{16}{{{y}_{0}}^{2}})({{y}_{0}}^{2}-12)$=$\frac{-12{{y}_{0}}^{4}+144{{y}_{0}}^{2}+768}{{{y}_{0}}^{2}}$>0.
${x}_{1}+{x}_{2}=\frac{-8{{y}_{0}}^{2}}{3{{y}_{0}}^{2}+16},{x}_{1}{x}_{2}=\frac{{{y}_{0}}^{4}-12{{y}_{0}}^{2}}{3{{y}_{0}}^{2}+16}$.
∴AB的中点坐标为$(\frac{-4{{y}_{0}}^{2}}{3{{y}_{0}}^{2}+16},\frac{\frac{3}{2}{{y}_{0}}^{3}}{3{{y}_{0}}^{2}+16})$,
∴AB的垂直平分线方程为$y-\frac{\frac{3}{2}{{y}_{0}}^{3}}{3{{y}_{0}}^{2}+16}=-\frac{{y}_{0}}{2}(x+\frac{4{{y}_{0}}^{2}}{3{{y}_{0}}^{2}+16})$,令x=0,得$y=\frac{-\frac{1}{2}{{y}_{0}}^{3}}{3{{y}_{0}}^{2}+16}$,
即N$(0,\frac{-\frac{1}{2}{{y}_{0}}^{3}}{3{{y}_{0}}^{2}+16})$,∴${k}_{MN}=\frac{-2{y}_{0}}{3{{y}_{0}}^{2}+16}$.
∵y0>0,∴${k}_{MN}=\frac{-2{y}_{0}}{3{{y}_{0}}^{2}+16}$=$\frac{-2}{3{y}_{0}+\frac{16}{{y}_{0}}}$$≥-\frac{\sqrt{3}}{12}$,当且仅当${y}_{0}=\frac{4\sqrt{3}}{3}$时取得等号.
∴直线MN的斜率的最小值为$-\frac{\sqrt{3}}{12}$.
点评 本题考查椭圆标准方程的求法,考查了直线与椭圆位置关系的应用,训练了利用基本不等式求最值,体现了整体运算思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5元 | B. | 4元 | C. | 1元 | D. | 4.5元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,0)∪(0,1) | D. | (-∞,0)∪(0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
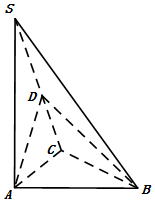 如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC
如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若?服从正态分布N(1,2),且P(?>2)=0.1,则P(0<?<2)=0.2 | |
| B. | 命题:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com