
分析 (1)求出a=2,b=1的函数f(x)的导数,求得单调区间,求得极值;
(2)求出g(x)的导数,由题意可得存在x>1,使2ax3-3ax2-2bx+b=0 成立.由a>0,则$\frac{b}{a}=\frac{{2{x^3}-3{x^2}}}{2x-1}$,
设$u(x)=\frac{{2{x^3}-3{x^2}}}{2x-1}(x>1)$,求出导数,判断单调性,即可得到所求范围.
解答 解:(1)当a=2,b=1时,$f(x)=(2+\frac{1}{x}){e^x}$,定义域为(-∞,0)∪(0,+∞).
所以$f'(x)=\frac{(x+1)(2x-1)}{x^2}{e^x}$.
令f′(x)=0,得${x_1}=-1,{x_2}=\frac{1}{2}$,列表
| x | (-∞,-1) | -1 | (-1,0) | $({0,\frac{1}{2}})$ | $\frac{1}{2}$ | $({\frac{1}{2},+∞})$ |
| f'(x) | + | 0 | - | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
点评 本题考查导数的运用:求单调区间和极值,主要考查函数的单调性的运用,考查运算能力,正确求导和构造函数是解题的关键.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{2}π}{3}$ | B. | $\frac{8\sqrt{2}π}{3}$ | C. | $\frac{32π}{3}$ | D. | $\frac{16π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | f(x)的极大值为f($\sqrt{3}$),极小值为f(-$\sqrt{3}$) | B. | f(x)的极大值为f(0),极小值为f(-3) | ||
| C. | f(x)的极大值为f(3),极小值为f(-3) | D. | f(x)的极大值为f(3),极小值为f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
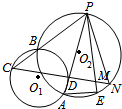 如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N.
如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知正三棱柱ABC-A1B1C1所有棱长均为a,D为BB1上一点,则三棱锥C1-ACD的体积为$\frac{{\sqrt{3}}}{12}{a^3}$.
如图,已知正三棱柱ABC-A1B1C1所有棱长均为a,D为BB1上一点,则三棱锥C1-ACD的体积为$\frac{{\sqrt{3}}}{12}{a^3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知BC为圆O的直径,点A为圆周上一点,AD⊥BC于点D,过点A作圆O的切线交BC的延长线于点P,过点B作BE垂直PA的延长线于点E.求证:
已知BC为圆O的直径,点A为圆周上一点,AD⊥BC于点D,过点A作圆O的切线交BC的延长线于点P,过点B作BE垂直PA的延长线于点E.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com