
[2013·广东高考]设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是( )
A.若α⊥β,m?α,n?β,则m⊥n
B.若α∥β,m?α,n?β,则m∥n
C.若m⊥n,m?α,n?β,则α⊥β
D.若m⊥α,m∥n,n∥β,则α⊥β
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源:2015数学一轮复习迎战高考:9-3变量间的相关关系与统计案例(解析版) 题型:选择题
[2013·杭州模拟]在2013年3月15日,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x和销售量y之间的一组数据如下表所示:
价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y(件) | 11 | 10 | 8 | 6 | 5 |
由散点图可知,销售量y与价格x之间有较好的线性相关关系,且回归直线方程是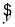 =-3.2x+
=-3.2x+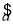 ,则
,则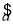 =( )
=( )
A.-24 B.35.6 C.40.5 D.40
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考:8-4直线与圆、圆与圆的位置关系(解析版) 题型:选择题
若圆O:x2+y2=4与圆C:x2+y2+4x-4y+4=0关于直线l对称,则直线l的方程是( )
A.x+y=0 B.x-y=0
C.x-y+2=0 D.x+y+2=0
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考:7-7立体几何中的向量方法(解析版) 题型:填空题
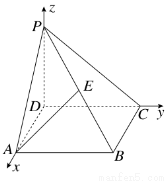
[2014·泉州模拟]如图,PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos〈 ,
,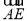 〉=
〉=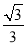 ,若以DA,DC,DP所在直线分别为x,y,z轴建立空间直角坐标系,则点E的坐标为________.
,若以DA,DC,DP所在直线分别为x,y,z轴建立空间直角坐标系,则点E的坐标为________.
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考:7-6空间向量及运算(解析版) 题型:选择题
[2013·重庆诊测]若向量a=(1,λ,2),b=(2,-1,2),且a与b的夹角余弦值为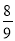 ,则λ等于( )
,则λ等于( )
A.2 B.-2 C.-2或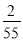 D.2或-
D.2或-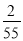
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考:7-4直线、平面平行的判定及性质(解析版) 题型:选择题
[2013·湖南娄底5月]平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥直线BD的充要条件是( )
A.AB∥CD B.AD∥CB
C.AB与CD相交 D.A,B,C,D四点共面
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考:7-2空间几何体的表面积和体积(解析版) 题型:填空题
[2012·辽宁高考]已知正三棱锥P-ABC,点P,A,B,C都在半径为 的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
的球面上,若PA,PB,PC两两相互垂直,则球心到截面ABC的距离为________.
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考:6-5合情推理与演绎推理(解析版) 题型:选择题
[2013·西安检测]给出下列三个类比结论.
①(ab)n=anbn与(a+b)n类比,则有(a+b)n=an+bn;
②loga(xy)=logax+logay与sin(α+β)类比,则有sin(α+β)=sinαsinβ;
③(a+b)2=a2+2ab+b2与(a+b)2类比,则有(a+b)2=a2+2a·b+b2.
其中结论正确的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考:5-2等差数列及其前n项和(解析版) 题型:选择题
[2014·天津市模拟]若等差数列{an}的前5项和S5=25,且a2=3,则a7=( )
A.12 B.13 C.14 D.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com