练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．如图，长方体ABCD-A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4．过E，F的平面α与此长方体的面相交，交线围成一个正方形
    （Ⅰ）在图中画出这个正方形（不必说出画法和理由）
    （Ⅱ）求平面α把该长方体分成的两部分体积的比值．

    分析 （Ⅰ）利用平面与平面平行的性质，可在图中画出这个正方形；
    （Ⅱ）求出MH=$\sqrt{E{H}^{2}-E{M}^{2}}$=6，AH=10，HB=6，即可求平面a把该长方体分成的两部分体积的比值．

    解答 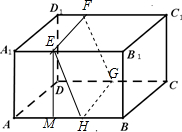解：（Ⅰ）交线围成的正方形EFGH如图所示；
    （Ⅱ）作EM⊥AB，垂足为M，则AM=A1E=4，EB1=12，EM=AA1=8．
    因为EFGH为正方形，所以EH=EF=BC=10，
    于是MH=$\sqrt{E{H}^{2}-E{M}^{2}}$=6，AH=10，HB=6．
    因为长方体被平面α分成两个高为10的直棱柱，
    所以其体积的比值为$\frac{9}{7}$．

    点评 本题考查平面与平面平行的性质，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．函数f（x）=cos（ωx+φ）的部分图象如图所示，则f（x）的单调递减区间为（　　）
    A．（kπ-$\frac{1}{4}$，kπ+$\frac{3}{4}$，），k∈zB．（2kπ-$\frac{1}{4}$，2kπ+$\frac{3}{4}$），k∈z
    C．（k-$\frac{1}{4}$，k+$\frac{3}{4}$），k∈zD．（$2k-\frac{1}{4}$，2k+$\frac{3}{4}$），k∈z

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．命题“?x0∈（0，+∞），lnx0=x0-1”的否定是（　　）
    A．?x0∈（0，+∞），lnx0≠x0-1B．?x0∉（0，+∞），lnx0=x0-1
    C．?x∈（0，+∞），lnx≠x-1D．?x∉（0，+∞），lnx=x-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知a≥b＞0，求证：2a3-b3≥2ab2-a2b．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若x，y满足约束条件$\left\{{\begin{array}{l}{x+y-5≤0}\\{2x-y-1≥0}\\{x-2y+1≤0}\end{array}}\right.$，则z=2x+y的最大值为8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．阅读如图的程序框图，运行相应的程序，则输出S的值为（　　）
    A．-10B．6C．14D．18

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在△ABC中，内角A，B，C所对的边分别为a，b，c．已知△ABC的面积为3$\sqrt{15}$，b-c=2，cosA=-$\frac{1}{4}$，则a的值为8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知A=$\frac{π}{4}$，b2-a2=$\frac{1}{2}$c2．
    （1）求tanC的值；
    （2）若△ABC的面积为3，求b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．如图，在四棱锥P-ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC=∠BAD=$\frac{π}{2}$，PA=AD=2，AB=BC=1．
    （1）求平面PAB与平面PCD所成二面角的余弦值；
    （2）点Q是线段BP上的动点，当直线CQ与DP所成的角最小时，求线段BQ的长．

    查看答案和解析>>

    同步练习册答案