
2
| ||
| 5 |
| 1 |
| 3 |
2
| ||
| 5 |
| 1-cos2A |
| ||
| 5 |
| sinA |
| cosA |
| 1 |
| 2 |
| sinB |
| cosB |
| 1 |
| 3 |
| tanA+tanB |
| 1-tanAtanB |
| ||||
1-
|
| 3π |
| 4 |
| a |
| sinA |
| b |
| sinB |
2
| ||
| 5 |
| ||
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 5 |
| ||
| 5 |
| ||
| 2 |
| 1 |
| 5 |


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
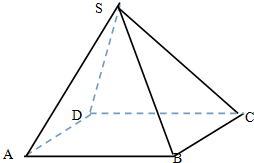 如图四棱锥S-ABCD中,底面是边长为2厘米的正方形,侧棱长都是2厘米.
如图四棱锥S-ABCD中,底面是边长为2厘米的正方形,侧棱长都是2厘米.查看答案和解析>>
科目:高中数学 来源: 题型:
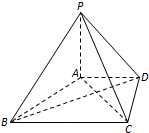 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| tanA+tanC |
| 3 |
| sinB |
| cosC |
| CD |
| DB |
查看答案和解析>>
科目:高中数学 来源: 题型:
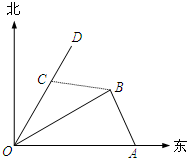 如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com