
| A. | k≤0 | B. | -1≤k≤0 | C. | k≥0 | D. | 0≤k≤1 |
分析 通过x的范围的讨论,转化不等式去掉绝对值以及绝对值的几何意义求出k的范围.
解答 解:若x=0,原不等式变化为1≥0恒成立,此时的k∈R;
若x>0,原不等式变化为k≤$\frac{|x+1|}{x}$=$\frac{x+1}{x}$=1+$\frac{1}{x}$恒成立,因为1+$\frac{1}{x}$>0,所以k≤1;
若x<0,原不等式变化为k≥$\frac{|x+1|}{x}$恒成立立,因为$\frac{|x+1|}{x}$<0,所以以k≥0.
综上所述,0≤k≤1.
故选:D.
点评 本题考查不等式的解法,函数的恒成立的应用,考查代数法,分类与整合的应用;也可以利用函数y=|x+1|和函数y=kx的图象求解.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±2 | B. | ±$\sqrt{5}$ | C. | ±3 | D. | ±5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(±\sqrt{3},0)$ | B. | $(0,±\sqrt{3})$ | C. | $(±\sqrt{3},0)$或$(±\sqrt{5},0)$ | D. | $(0,±\sqrt{3})$或$(±\sqrt{5},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | [0,1) | C. | (-∞,-1)∪[0,1) | D. | (-1,0]∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | B. | $\frac{x^2}{24}$-$\frac{y^2}{12}$=1 | C. | $\frac{x^2}{3}$-$\frac{y^2}{6}$=1 | D. | $\frac{x^2}{6}$-$\frac{y^2}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
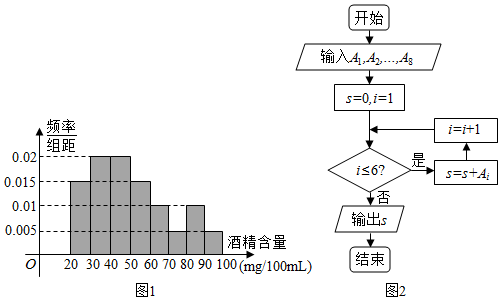
| A. | 24480 | B. | 24380 | C. | 23040 | D. | 23140 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com