
分析 (1)由椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(1,$\frac{3}{2}$),且椭圆C关于直线x=c对称的图形过坐标原点,求出a,b,c,椭圆方程可求;
(2)线l过点($\frac{1}{2}$,0)且斜率不为零,故可设其方程为x=my+$\frac{1}{2}$,和椭圆方程联立,把MA的斜率用直线l的斜率表示,由基本不等式求得范围.
解答 解:(1)∵椭圆C过点(1,$\frac{3}{2}$),∴$\frac{1}{{a}^{2}}$+$\frac{9}{4{b}^{2}}$=1,①…(1分)
∵椭圆C关于直线x=c对称的图形过坐标原点,∴a=2c,…(2分)
∴${b}^{2}=\frac{3}{4}{a}^{2}$,②…(3分)
由①②得a=2,b=$\sqrt{3}$,…(4分)
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$…(5分)
(2)依题意,直线l过点($\frac{1}{2}$,0)且斜率不为零,故可设其方程为x=my+$\frac{1}{2}$…(7分)
联立方程组消去x,并整理得4(3m2+4)y2+12my-45=0(6分)
设E(x1,y1),F(x2,y2),M(x0,y0),则
∴y1+y2=-$\frac{3m}{3{m}^{2}+4}$,(7分)
∴y0=-$\frac{3m}{2(3{m}^{2}+4)}$,x0=$\frac{2}{3{m}^{2}+4}$,
∴k=$\frac{m}{4{m}^{2}+4}$,(9分)
①当m=0时,k=0;(10分)
②当m≠0时,k=$\frac{1}{4m+\frac{4}{m}}$,
∵|4m+$\frac{4}{m}$|=4|m|+$\frac{4}{|m|}$≥8,∴0<|k|≤$\frac{1}{8}$,∴-$\frac{1}{8}$≤k≤$\frac{1}{8}$且k≠0.(11分)
综合①②可知直线MA的斜率k的取值范围是:-$\frac{1}{8}$≤k≤$\frac{1}{8}$.…(12分)
点评 本题考查了椭圆方程的求法,考查了直线与圆锥曲线间的关系,体现了“设而不求”的解题思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
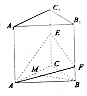 如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.
如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{32}$ | B. | -$\frac{1}{28}$ | C. | $\frac{1}{28}$ | D. | -$\frac{1}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0} | B. | (-1,0) | C. | {-1,0} | D. | (-3,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校从参加高二年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段后画出如下频率分布直方图.观察图形的信息,回答下列问题:这次考试的中位数为73.3 (结果保留一位小数).
某校从参加高二年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段后画出如下频率分布直方图.观察图形的信息,回答下列问题:这次考试的中位数为73.3 (结果保留一位小数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com