
分析 由直线l不经过第四象限,得到x≤0,y≥0,求出k的最小值,经过原点时k最大,求出k的最大值,则实数k的取值范围可求.
解答 解:∵直线l:y-1=k(x-$\sqrt{3}$)不经过第四象限,则x≤0,y≥0,
∴k的最小值为kmin=0,
经过原点时k最大,
∴k的最大值为kmax=$\frac{y-1}{x-\sqrt{3}}$=$\frac{0-1}{0-\sqrt{3}}=\frac{\sqrt{3}}{3}$,
则实数k的取值范围是[0,$\frac{\sqrt{3}}{3}$].
故答案为:[0,$\frac{\sqrt{3}}{3}$].
点评 本题考查直线的斜率的取值范围的求法,是基础题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
 一锥体的三视图如图所示,则该棱锥的最长棱的棱长为( )
一锥体的三视图如图所示,则该棱锥的最长棱的棱长为( )| A. | $\sqrt{33}$ | B. | $\sqrt{17}$ | C. | $\sqrt{41}$ | D. | $\sqrt{42}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
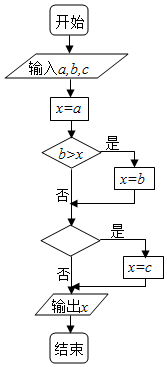 执行如图的程序框图,则判断框可填入和输出的结果分别是( )
执行如图的程序框图,则判断框可填入和输出的结果分别是( )| A. | c>x;a,b,c中最小的 | B. | c=x;a,b,c中最小的 | ||
| C. | c<x;a,b,c中最大的 | D. | c>x;a,b,c中最大的 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 身高x为解释变量,体重y为预报变量 | |
| B. | y与x具有正的线性相关关系 | |
| C. | 回归直线过样本点的中心($\overline x$,$\overline y$) | |
| D. | 若该大学某女生身高为170cm,则她的体重必为58.79kg |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com