
分析 (Ⅰ)由$a_{n+1}^2=\frac{1}{3}a_n^2+\frac{2}{3}{a_n}$,得${{a}_{n+1}}^{2}-1=\frac{1}{3}({{a}_{n}}^{2}+2{a}_{n}-3)=\frac{1}{3}({a}_{n}-1)$(an+3),从而$\frac{1-{a}_{n+1}}{1-{a}_{n}}=\frac{1}{3}•\frac{{a}_{n}+3}{{a}_{n+1}+1}$>0,进而an+1<1,由${a}_{1}=\frac{1}{2}<1$,得0<an<1,(n∈N*),由此证明0<an<an+1<1(n∈N*).
(Ⅱ)由$\frac{1-{a}_{n+1}}{1-{a}_{n}}$=$\frac{1}{3}•\frac{{a}_{n}+3}{{a}_{n+1}+1}$<$\frac{7}{9}$,得1-an=(1-a1)×$\frac{1-{a}_{2}}{1-{a}_{1}}$×$\frac{1-{a}_{3}}{1-{a}_{2}}$×…×$\frac{1-{a}_{n}}{1-{a}_{n-1}}$$<\frac{1}{2}•(\frac{7}{9})^{n-1}$,由此能证明${a_1}+{a_2}+…+{a_n}>n-\frac{9}{4}$(n∈N*).
解答 证明:(Ⅰ)由$a_{n+1}^2=\frac{1}{3}a_n^2+\frac{2}{3}{a_n}$,
得${{a}_{n+1}}^{2}-1=\frac{1}{3}({{a}_{n}}^{2}+2{a}_{n}-3)=\frac{1}{3}({a}_{n}-1)$(an+3),
即$({a}_{n+1}-1)({a}_{n+1}+1)=\frac{1}{3}({a}_{n}-1)({a}_{n}+3)$,
得$\frac{1-{a}_{n+1}}{1-{a}_{n}}=\frac{1}{3}•\frac{{a}_{n}+3}{{a}_{n+1}+1}$>0,
∴$1-{a}_{n+1}=(1-{a}_{1})×\frac{1-{a}_{2}}{1-{a}_{1}}×\frac{1-{a}_{3}}{1-{a}_{2}}×…×$$\frac{1-{a}_{n+1}}{1-{a}_{n}}$
=$\frac{1}{2}×\frac{1}{{3}^{n}}×\frac{{a}_{1}+3}{{a}_{2}+1}×\frac{{a}_{2}+3}{{a}_{3}+1}×…×\frac{{a}_{n}+3}{{a}_{n+1}+1}$>0,
∴an+1<1,
又${a}_{1}=\frac{1}{2}<1$,∴0<an<1,(n∈N*),
∴${{a}_{n+1}}^{2}-{{a}_{n}}^{2}$=$\frac{2}{3}{a}_{n}$(1-an)>0,
∴an+1>an,
综上,得:0<an<an+1<1(n∈N*).
(Ⅱ)由(Ⅰ)知:
$\frac{1-{a}_{n+1}}{1-{a}_{n}}$=$\frac{1}{3}•\frac{{a}_{n}+3}{{a}_{n+1}+1}$<$\frac{1}{3}•\frac{{a}_{n}+3}{{a}_{n}+1}$=$\frac{1}{3}$(1+$\frac{2}{{a}_{n}+1}$)≤$\frac{1}{3}(1+\frac{2}{{a}_{1}+1})$=$\frac{7}{9}$,
则n≥2时,1-an=(1-a1)×$\frac{1-{a}_{2}}{1-{a}_{1}}$×$\frac{1-{a}_{3}}{1-{a}_{2}}$×…×$\frac{1-{a}_{n}}{1-{a}_{n-1}}$$<\frac{1}{2}•(\frac{7}{9})^{n-1}$,
∴(1-a1)+(1-a2)+(1-a3)+…+(1-an)<$\frac{1}{2}+\frac{1}{2}•(\frac{7}{9})+\frac{1}{2}(\frac{7}{9})^{2}+…+\frac{1}{2}•(\frac{7}{9})^{n-1}$,
即n-(a1+a2+a3+…+an)<$\frac{1}{2}•\frac{1-(\frac{7}{9})^{n}}{1-\frac{7}{9}}$=$\frac{9}{4}$[1-($\frac{7}{9}$)n]$<\frac{9}{4}$,
∴${a_1}+{a_2}+…+{a_n}>n-\frac{9}{4}$(n∈N*).
点评 本题考查数列与不等式的综合题,是中档题,解题时要认真审题,注意放缩法、不等式性质、数列知识的合理运用.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
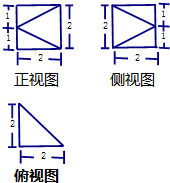
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{8\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3] | B. | [2,3] | C. | (-∞,0)∪(0,2] | D. | (-∞,-1)∪[0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
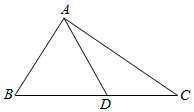 如图,D是直角三角形△ABC斜边BC上一点,AC=$\sqrt{3}$DC.
如图,D是直角三角形△ABC斜边BC上一点,AC=$\sqrt{3}$DC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com