Question

4．如图，是某多面体的三视图，则该多面体的体积为（　　）

• A． $\frac{4}{3}$
• B． $\frac{8}{3}$
• C． $\frac{16}{3}$
• D． $\frac{8\sqrt{2}}{3}$

Answer 1

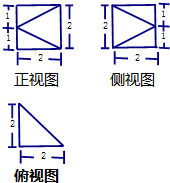
分析 根据几何体的三视图，得出该几何体为棱长是2的正方体，截去两个相同的三棱锥，再截去一个三棱柱（底面直角三角形的直角边为2和2，高为2）而得到，画出它的直观图，即可求其体积．

解答 解：根据几何体的三视图，得；
该几何体为棱长是2的正方体，截去两个相同的三棱锥（底面直角三角形的直角边为2和2，高为1）；
，再截去一个三棱柱（底面直角三角形的直角边为2和2，高为2）而得到，其直观图如图所示，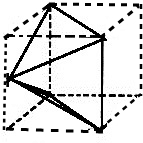
∴该多面体的体积为：2×2×2-2×$2×\frac{1}{2}×2$-2×（2×$\frac{1}{3}$×$2×\frac{1}{2}×1$）=$\frac{8}{3}$．
故选：B．

点评 本题考查了空间几何体的三视图的应用问题，解题的关键是画出几何体的直观图，是中档题．