
分析 (1)当k=1时,有${a_n}+{a_{n+1}}={2^n}$,得${a_{n+1}}-\frac{1}{3}•{2^{n+1}}=-({a_n}-\frac{1}{3}•{2^n})$,利用等比数列的通项公式即可得出.
(2)①证明:当k=4时,有an+4-an=8(n∈N*),n=4m(m∈N*)时,a4(m+1)-a4m=8,所以{a4m}为等差数列;同理可得:n=4m-1(m∈N*)时,a4(m+1)-1-a4m-1=8,所以{a4m-1}为等差数列;n=4m-2(m∈N*)时,n=4m-3(m∈N*)时,都为等差数列;可得an+1-an=2,所以数列{an}为等差数列.
②由①知,an=2n+2,则${S_n}={n^2}+3n$(n∈N*);由${({S_n}+1)^2}-\frac{3}{2}{a_n}+33={k^2}$,得(n2+3n+1)2-3(n-10)=k2.对n,k分类讨论:当n=10时,k=131;当n>10时,则k<n2+3n+1,因为k2-(n2+3n)2=2n2+3n+31>0,所以k>n2+3n;不存在.n≤9时验证即可得出.
解答 解:(1)当k=1时,有${a_n}+{a_{n+1}}={2^n}$,得${a_{n+1}}-\frac{1}{3}•{2^{n+1}}=-({a_n}-\frac{1}{3}•{2^n})$,
令${c_n}={a_n}-\frac{1}{3}•{2^n}$,${c_1}={a_1}-\frac{2}{3}=\frac{1}{3}≠0$,所以$\frac{{{c_{n+1}}}}{c_n}=-1$,
所以数列{cn}是首项为$\frac{1}{3}$,公比为-1的等比数列;所以${c_n}=\frac{1}{3}{(-1)^{n-1}}$,
即${a_n}-\frac{1}{3}•{2^n}=\frac{1}{3}{(-1)^{n-1}}$,所以${a_n}=\frac{1}{3}•[{{2^n}+{{(-1)}^{n-1}}}]$(n∈N*).(4分)
(2)①证明:当k=4时,有an+4-an=8(n∈N*),n=4m(m∈N*)时,a4(m+1)-a4m=8,所以{a4m}为等差数列;a4m=10+8(m-1)=8m+2(m∈N*);n=4m-1(m∈N*)时,a4(m+1)-1-a4m-1=8,所以{a4m-1}为等差数列;a4m-1=8+8(m-1)=8m(m∈N*);n=4m-2(m∈N*)时,a4(m+1)-2-a4m-2=8,所以{a4m-2}为等差数列;a4m-2=6+8(m-1)=8m-2(m∈N*);n=4m-3(m∈N*)时,a4(m+1)-3-a4m-3=8,所以{a4m-3}为等差数列;a4m-3=4+8(m-1)=8m-4(m∈N*);
所以an=2n+2(n∈N*),an+1-an=2,所以数列{an}为等差数列.(10分)
②由①知,an=2n+2,则${S_n}={n^2}+3n$(n∈N*);
由${({S_n}+1)^2}-\frac{3}{2}{a_n}+33={k^2}$,得(n2+3n+1)2-3(n-10)=k2;
当n=10时,k=131;
当n>10时,则k<n2+3n+1,因为k2-(n2+3n)2=2n2+3n+31>0,所以k>n2+3n;
从而n2+3n<k<n2+3n+1,因为k和n为正整数,所以不存在正整数k;
当n<10时,则k>n2+3n+1,因为k为正整数,所以k≥n2+3n+2,
从而(n2+3n+1)2-3(n-10)≥(n2+3n+2)2,即2n2+9n-27≤0,
因为n为正整数,所以n=1或n=2;
当n=1时,k2=52,k不是正整数;当n=2时,k2=145,k不是正整数;
综上,满足题意的所有正整数k和n分别为n=10,k=131.(16分)
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式求和公式、分类讨论方法,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $-\frac{7}{8}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{3-2\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,D为BC的中点,E为AD的中点,直线BE与边AC交于点F,若AD=BC=6,则$\overrightarrow{AB}•\overrightarrow{CF}$=-18.
如图,在△ABC中,D为BC的中点,E为AD的中点,直线BE与边AC交于点F,若AD=BC=6,则$\overrightarrow{AB}•\overrightarrow{CF}$=-18.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
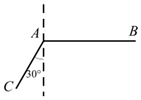 如图,当甲船位于A处时获悉,在其正东方向相距10海里的B处有个艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距6海里的C处的乙船,乙船立即朝北偏东(θ+30°)的方向沿直线前往B处营救,则sinθ的值为$\frac{5\sqrt{3}}{14}$.
如图,当甲船位于A处时获悉,在其正东方向相距10海里的B处有个艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距6海里的C处的乙船,乙船立即朝北偏东(θ+30°)的方向沿直线前往B处营救,则sinθ的值为$\frac{5\sqrt{3}}{14}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 57 | B. | 58 | C. | 62 | D. | 63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com