
���� ��1����M=$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$�����ݾ���任���з����飬�������a��b��c��d��ֵ�����M��
��2��Բ��Ϊֱ��$��sin��\frac{��}{3}-�ȣ�$=$\frac{\sqrt{3}}{2}$�뼫����Ľ��㣬���=0���æ�=1���������Բ�����꼰�뾶���������ԲC�ļ����귽�̣�
��� �⣺��1����M=$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$����$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$$[\begin{array}{l}{1}\\{1}\end{array}]$=3$[\begin{array}{l}{1}\\{1}\end{array}]$����$\left\{\begin{array}{l}{a+b=3}\\{c+d=3}\end{array}\right.$��
��$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$$[\begin{array}{l}{-1}\\{2}\end{array}]$=$[\begin{array}{l}{9}\\{15}\end{array}]$���ã�$\left\{\begin{array}{l}{-a+2b=9}\\{-c+2d=3}\end{array}\right.$��
���a=-1��b=4��c=-3��d=6��
��M=$[\begin{array}{l}{-1}&{4}\\{-3}&{6}\end{array}]$��
��2����ΪԲ��Ϊֱ��$��sin��\frac{��}{3}-�ȣ�$=$\frac{\sqrt{3}}{2}$�뼫����Ľ��㣬
�������=0���æ�=1����Բ��Ϊ��1��0����
��Բ��C������P��$\sqrt{3}$��$\frac{��}{6}$����
����Բ�İ뾶r=$\sqrt{3+1-2\sqrt{3}cos\frac{��}{6}}$=1��
����Բ��ԭ�㣬�伫���귽�̦�=2cos�ȣ�
���� ���⿼�����ı任�����鼫����ϵ��ֱ����Բλ�ù�ϵ������ת��˼�룬�����е��⣮


 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��-1�� | B�� | ��1��1�� | C�� | ��1��$\sqrt{3}}$�� | D�� | ��${\sqrt{3}$��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
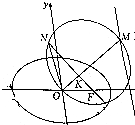 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����ҽ���ΪF��������Ϊ$\frac{\sqrt{2}}{2}$����ֱ��2x+y-3=0����ԲC���У�
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����ҽ���ΪF��������Ϊ$\frac{\sqrt{2}}{2}$����ֱ��2x+y-3=0����ԲC���У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com