
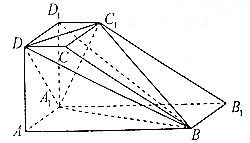
 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.分析 (Ⅰ)连接AD1,B1D1,由已知可得A1D⊥AD1,再由AB⊥平面ADD1,得AB⊥A1D,由此可得A1D⊥平面ABD1,即A1D⊥BD1,在平面A1C1 B1内,通过解直角三角形可得A1C1⊥B1D1,即BB1⊥平面A1C1 B1,进一步得到BB1⊥A1C1,再由线面垂直的判定可得BD1⊥平面A1C1D;
(Ⅱ)多面体BDC1A1D1可看作是有公共底面DA1C1 的两个三棱锥构成的组合体,求出△A1DC1的面积S,由(Ⅰ)知,BD1⊥面A1DC1,然后由棱锥体积公式求得多面体BDC1A1D1的体积.
解答 (Ⅰ)证明:连接AD1,B1D1,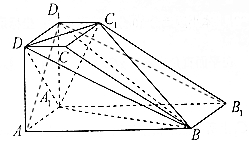
∵AA1D1D是正方形,∴A1D⊥AD1,
又∵AB⊥平面ADD1,A1D?平面ADD1,∴AB⊥A1D.
因此,A1D⊥平面ABD1,∴A1D⊥BD1,
又在平面A1C1 B1内,Rt△C1D1A1∽Rt△B1A1D1,
∴∠D1A1C1+∠A1D1B1=∠D1A1C1+∠D1C1A1=90°,即A1C1⊥B1D1.
又BB1⊥平面A1C1 B1,A1C1?平面A1C1B1,
∴BB1⊥A1C1,
因此,A1C1⊥平面BB1D1,∴A1C1⊥BD1,
又A1D∩A1C1=A1,∴BD1⊥平面A1C1D;
(Ⅱ)解:多面体BDC1A1D1可看作是有公共底面DA1C1 的两个三棱锥构成的组合体,
在Rt△DD1C1 中,$D{C}_{1}=\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$,在Rt△DAA1 中,$D{A}_{1}=\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2}$,
在Rt△A1D1C1 中,${A}_{1}{C}_{1}=\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$,∴△A1DC1为等腰三角形,且面积S=$\sqrt{6}$,
由(Ⅰ)知,BD1⊥面A1DC1,且$B{D}_{1}=\sqrt{{D}_{1}{A}^{2}+{A}_{1}{B}^{2}}=2\sqrt{6}$.
∴多面体BDC1A1D1的体积V=$\frac{1}{3}S×B{D}_{1}=\frac{1}{3}×\sqrt{6}×2\sqrt{6}=4$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2寸 | B. | 3寸 | C. | 4寸 | D. | 5寸 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
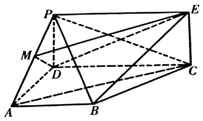 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
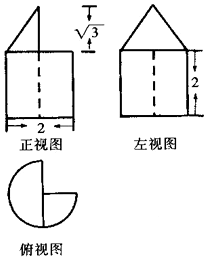
| A. | $\frac{9+\sqrt{3}}{6}$π | B. | $\frac{6+\sqrt{3}}{6}$π | C. | $\frac{3+\sqrt{3}}{6}$π | D. | $\frac{12+\sqrt{3}}{6}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在△ABC中,角A、B、C所对的边分别是a、b、c,已知$\sqrt{3}a=2csinA$且c<b.
在△ABC中,角A、B、C所对的边分别是a、b、c,已知$\sqrt{3}a=2csinA$且c<b. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,6] | B. | [1,4] | C. | [2,4] | D. | [2,6] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com