
分析 (Ⅰ)求导数,确定函数的单调性,即可求函数f(x)的最小值;
(Ⅱ)设F(x)=ax2+f′(x)(a∈R),求导数,对a分类讨论,利用导数的正负,即可讨论函数F(x)的单调性;
(Ⅲ)$k=\frac{{f'({x_2})-f'({x_1})}}{{{x_2}-{x_1}}}=\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}$,要证明${x_1}<\frac{1}{k}<{x_2}$,即证${x_1}<\frac{{{x_2}-{x_1}}}{{ln{x_2}-ln{x_1}}}<{x_2}$,等价于$1<\frac{{\frac{x_2}{x_1}-1}}{{ln\frac{x_2}{x_1}}}<\frac{x_2}{x_1}$,令$t=\frac{x_2}{x_1}$(由x1<x2,知t>1),则只需证$1<\frac{t-1}{lnt}<t$,由t>1,知lnt>0,故等价于lnt<t-1<tlnt(t>1).
解答 解:(Ⅰ)f'(x)=lnx+2(x>0),…(1分)
令f'(x)=0,得$x=\frac{1}{e^2}$,
当$x∈({0,\frac{1}{e^2}})$时,f'(x)<0;当$x∈({\frac{1}{e^2},+∞})$时,f'(x)>0.
则f(x)在$({0,\frac{1}{e^2}})$内递减,在$({\frac{1}{e^2},+∞})$内递增,…(2分)
所以当$x=\frac{1}{e^2}$时,函数f(x)取得最小值,且$f{(x)_{min}}=f({\frac{1}{e^2}})=\frac{1}{e^2}({ln\frac{1}{e^2}+1})=-\frac{1}{e^2}$…(3分)
(Ⅱ)F(x)=ax2+lnx+2,$F'(x)=2ax+\frac{1}{x}=\frac{{2a{x^2}+1}}{x}$(x>0),…(4分)
当a≥0时,恒有F'(x)>0,F(x)在区间(0,+∞)内是增函数;…(5分)
当a<0时,令F'(x)>0,即2ax2+1>0,解得$0<x<\sqrt{-\frac{1}{2a}}$,
令F'(x)<0,即2ax2+1<0,解得$x>\sqrt{-\frac{1}{2a}}$,…(6分)
综上,当a≥0时,F(x)在区间(0,+∞)内是增函数,当a<0时,F(x)在$({0,\sqrt{-\frac{1}{2a}}})$内单调递增,在$({\sqrt{-\frac{1}{2a}},+∞})$内单调递减.…(7分)
(Ⅲ)证明:$k=\frac{{f'({x_2})-f'({x_1})}}{{{x_2}-{x_1}}}=\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}$,要证明${x_1}<\frac{1}{k}<{x_2}$,
即证${x_1}<\frac{{{x_2}-{x_1}}}{{ln{x_2}-ln{x_1}}}<{x_2}$,…(8分)
等价于$1<\frac{{\frac{x_2}{x_1}-1}}{{ln\frac{x_2}{x_1}}}<\frac{x_2}{x_1}$,令$t=\frac{x_2}{x_1}$(由x1<x2,知t>1),
则只需证$1<\frac{t-1}{lnt}<t$,由t>1,知lnt>0,
故等价于lnt<t-1<tlnt(t>1)(*)…(9分)
①设g(t)=t-1-lnt(t>1),则$g'(t)=1-\frac{1}{t}>0$(t>1),
所以g(t)在(1,+∞)内是增函数,
当t>1时,g(t)=t-1-lnt>g(1)=0,所以t-1>lnt;…(10分)
②设h(t)=tlnt-(t-1)(t>1),则h'(t)=lnt>0(t>1),
所以h(t)在(1,+∞)内是增函数,
所以当t>1时,h(t)=tlnt-(t-1)>g(1)=0,即tlnt>t-1(t>1).…(11分)
由①②知(*)成立,所以${x_1}<\frac{1}{k}<{x_2}$.…(12分)
点评 本题考查导数知识的综合运用,考查函数的单调性与最值,考查不等式的证明,考查分类讨论的数学思想,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | -2 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
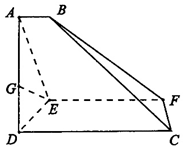 如图,已知梯形CDEF与△ADE所在的平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9,CD=12,连接BC,BF.
如图,已知梯形CDEF与△ADE所在的平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9,CD=12,连接BC,BF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
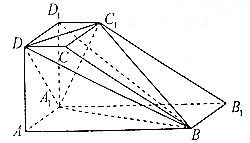 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com