
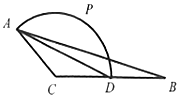
 已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点.
已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点.分析 (1)在三角形ABC中,利用余弦定理求出cos∠ACB的值,进而确定出∠ACB度数,在三角形ACD中求出AD的长即可;
(2)设PA=m,PD=n,由题意求出∠APD度数,在三角形APD中,利用余弦定理列出关系式,再利用基本不等式求出mn的范围,进而确定出m2+n2的范围,即可确定出所求式子范围.
解答 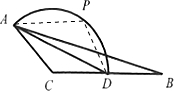 解:(1)∵△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点,
解:(1)∵△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点,
∴由余弦定理得:cos∠ACB=$\frac{4+16-28}{2×2×4}$=-$\frac{1}{2}$,
∴∠ACB=$\frac{2π}{3}$,
又AC=CD=2,
∴AD=2×2×sin$\frac{π}{3}$=2$\sqrt{3}$;
(2)连接AP,PD,如图所示,
设PA=m,PD=n,由题意:∠APD=$\frac{1}{2}$(2π-$\frac{2π}{3}$)=$\frac{2π}{3}$,
则在△APD中,m2+n2=12-mn,
又m2+n2≥2mn,
∴12-mn≥2mn,
解得:mn≤4,
又mn>0,
∴0<mn≤4,
则8≤m2+n2<12.
点评 此题考查了余弦定理,基本不等式的应用,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{64},1]$ | B. | $[\frac{1}{8},1]$ | C. | $(\frac{1}{64},1)$ | D. | $(\frac{1}{8},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
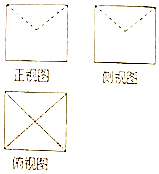 某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件 | |
| B. | 已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有$\frac{1}{{x}^{2}}$<$\frac{1}{{x}^{3}}$,则p∧(¬q)是真命题 | |
| C. | 命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0” | |
| D. | 从匀速传递的生产流水线上,质检员每隔5分钟从中抽取一件产品进行某项指标检测,这是分成抽样 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com