
| x | 1 | 2 | 3 | 4 |
| f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
分析 (1)把给出的三个模型分别验证,即可找出一个比较适合的模型;
(2)利用(1)的模型,先计算出预计的2014的产量,再去掉减少30%即可得出.
解答 解:(1)符合条件的是f(x)=ax+b,
若模型为f(x)=2x+a,则由f(1)=2+a=4,得a=2,即f(x)=2x+2,
此时f(2)=6,f(3)=10,f(4)=18,与已知相差太大,不符合.
若模型为f(x)=log${\;}_{\frac{1}{2}}$x+a,则f(x)是减函数,与已知不符合.
由已知得$\left\{\begin{array}{l}{a+b=4}\\{3a+b=7}\end{array}\right.$,解得a=$\frac{3}{2}$,b=$\frac{5}{2}$,
∴f(x)=$\frac{3}{2}$x+$\frac{5}{2}$,(x=1,2,…,6,7)经验证x=2,4,符合的比较好.
(2)∵2014年预计年产量为f(7)=$\frac{3}{2}×7+\frac{5}{2}$=13,∴13×(1-30%)=9.1,
即确定2014年的年产量约为9.1万件.
点评 熟练掌握建立模型的方法、不同函数模型的单调性等性质及正确计算是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
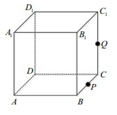 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是①②⑤(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是①②⑤(写出所有正确命题的编号).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2x | B. | f(x)=lnx | C. | f(x)=x3 | D. | f(x)=cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com