
| A. | (-∞,$\frac{5}{2}$) | B. | (-$\frac{5}{2}$,+∞) | C. | ($\frac{5}{2}$,+∞) | D. | (-1,+∞) |
分析 判断f(x)的单调性,作出f(x)的函数图象,得出f(x)=m的根的分别情况,从而得出关于m的方程的根的分别区间,列不等式解出t.
解答 解:f′(x)=3x2-3x=3x(x-1),
∴当x<0或x>1时f′(x)>0,当0<x<1时,f′(x)<0,
∴f(x)在(-∞,0)上单调递增,在(0,1)上单调递减,在(1,+∞)上单调递增,
∴当x=0时,f(x)取得极大值f(0)=0,当x=1时,f(x)取得极小值f(1)=-$\frac{1}{2}$.
作出f(x)的函数图象如图所示: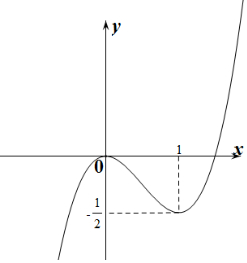
设f(x)=m,由图象可知:
当m<-$\frac{1}{2}$或m>0时,方程f(x)=m只有1解,
当m=-$\frac{1}{2}$或m=0时,方程f(x)=m有2解,
当-$\frac{1}{2}$<m<0时,方程f(x)=m有3解,
∵程f2(x)+tf(x)+1=0有四个实数根,
∴关于m的方程m2+tm+1=0在(-∞,-$\frac{1}{2}$)和(-$\frac{1}{2}$,0)上各有1个零点.
∴$\frac{1}{4}$-$\frac{1}{2}$t+1<0,
解得:t>$\frac{5}{2}$.
故选C.
点评 本题考查了方程根与函数图象的关系,函数的单调性判断与极值计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在正方形ABCD中,点E在边AD上(端点除外),现将△ABE沿直线BE翻折至△A′BE,连结A′C、A′D,记二面角A′-BE-C为α(0<α<π),则( )
在正方形ABCD中,点E在边AD上(端点除外),现将△ABE沿直线BE翻折至△A′BE,连结A′C、A′D,记二面角A′-BE-C为α(0<α<π),则( )| A. | 存在α,使得A′E⊥面A′BC | B. | 存在α,使得A′B⊥面A′CD | ||
| C. | 存在α,使得A′E⊥面A′CD | D. | 存在α,使得A′B⊥面A′DE |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinθ-cosθ | B. | cosθ-sinθ | C. | ±(sinθ-cosθ) | D. | sinθ+cosθ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某学校研究性学习小组对该校高二(1)班n名学生视力情况进行调查,得到如图所的频率分布直方图,已知视力在4.0~4.4范围内的学生人数为24人,视力在5.0~5.2范围内为正常视力,视力在3.8~4.0范围内为严重近视.
某学校研究性学习小组对该校高二(1)班n名学生视力情况进行调查,得到如图所的频率分布直方图,已知视力在4.0~4.4范围内的学生人数为24人,视力在5.0~5.2范围内为正常视力,视力在3.8~4.0范围内为严重近视.| 是否近视/年级名次 | 前10名 | 后10名 |
| 近视 | 9 | 7 |
| 不近视 | 1 | 3 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某学校研究性学习小组对该校高二(1)班n名学生视力情况进行调查,得到如图的频率分布直方图,已知视力在4.0~4.4范围内的学生人数为24人,视力在5.0~5.2范围内为正常视力,视力在3.8~4.0范围内为严重近视.
某学校研究性学习小组对该校高二(1)班n名学生视力情况进行调查,得到如图的频率分布直方图,已知视力在4.0~4.4范围内的学生人数为24人,视力在5.0~5.2范围内为正常视力,视力在3.8~4.0范围内为严重近视.| 是否近视/年级名次 | 前10名 | 后10名 |
| 近视 | 9 | 7 |
| 不近视 | 1 | 3 |
| P(k2≥k | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {0,1,2} | C. | {x|0≤x<3} | D. | {x|0≤x≤3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com