练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．空气质量指数（简称AQI）是定量描述空气质量状况的指数，其数值越大说明空气污染越严重，为了及时了解空气质量状况，广东各城市都设置了实时监测站．如表是某网站公布的广东省内21个城市在2014年12月份某时刻实时监测到的数据：
    城市 AQI数值城市 AQI数值城市 AQI数值城市 AQI数值城市 AQI数值城市 AQI数值城市 AQI数值
    广州118东莞137中山95江门78云浮76茂名107揭阳80
    深圳94珠海95湛江75潮州94河源124肇 庆48清远47
    佛山160惠州113汕头88汕尾74阳江112韶关68梅州84
    （1）请根据表中的数据，完成下列表格：
    空气质量优质良好轻度污染中度污染
    AQI值范围[0，50）[50，100）[100，150）[150，200）
    城市个数    
    （2）统计部门从空气质量“良好”和“轻度污染”的两类城市中采用分层抽样的方式抽取6个城市，省环保部门再从中随机选取3个城市组织专家进行调研，则选取的3个城市中至少有2个城市空气质量“良好”的概率是多少？

    分析 （1）根据频率分布的表的知识，填表即可
    （2）先求出由分层抽样方法抽取“良”、“轻度污染“，利用排列组合求出抽取3个城市的所有基本事件，并从中找出至少有2个城市空气质量“良好”的，利用基本事件个数比求概率．

    解答 解：（1）根据数据，完成表格如下：

    空气质量优质良好轻度污染中度污染
    AQI值范围[0，50）[50，100）[100，150）[150，200）
    城市频数21261
    …（4分）
    按分层抽样的方法，从“良好”类城市中抽取n1=$\frac{12}{12+6}$×6=4个  …（5分）
    从“轻度污染”类城市中抽取n2=$\frac{6}{12+6}×6$=2个，…（6分）
    现从这6个城市选取3个城市，所有的选取可能为：C63=20种…（7分）
    其中至少有2个城市空气质量“良好”的选取可能为：C42C21+C43C20=16种…（8分）
    故从6个城市选出的3个城市至少有2个城市空气质量“良好”的概率P=$\frac{16}{20}$=$\frac{4}{5}$…（10分）

    点评 本题考查了分层抽样方法及古典概型的概率计算，考查了学生搜集处理数据的能力，综合性较强，属于中档题

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

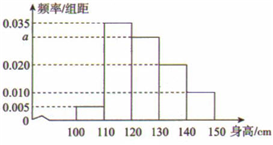    9．从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．若要从身高在[120，130），[130，140），[140，150]三组内的学生中，用分层抽样的方法选取18人参加一项活动．
    （1）求a的值
    （2）求从身高在[140，150]内的学生中选取的人数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

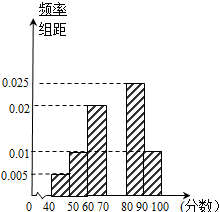    10．某校从高一年级学生中随机抽取40名学生，将他们的期末考试物理成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]后得到如图的频率分布直方图．
    （1）求成绩落在[70，80）上的频率，并补全这个频率分布直方图；
    （2）利用这个频率分布直方图求40名学生物理成绩的中位数；
    （3）若该校高一年级共有学生840人，试估计该校高一年级期中考试物理成绩不低于60分的人数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．下列命题中：
     ①回归直线除了经过样本点的中心，还至少经过一个样本点；
     ②将一组数据中的每个数都减去同一个数后，平均值有变化，方差没有变化；
    ③对分类变量X与Y，它们的随机变量K2的观测值k越小，“X与Y有关系”的把握程度越大；
     ④比较两个模型的拟合效果时，如果模型残差平方和越小，则相应的相关指数R2越大，该模型拟合的效果越好．
    其中正确命题的序号为②④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知函数f（x）=|ln（x-1）|，若实数a，b（a＜b）满足f（a）=f（b），则-a+5b的取值范围为（　　）
    A．（5，8）B．（8，9）C．（5，9）D．（8，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．若指数函数f（x）的图象过点（2，4），则f（4）=16．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=sinxcosx+cos2x-$\frac{1}{2}$．
    （1）求f（x）的最小正周期；
    （2）求f（x）的单调递减区间；
    （3）若函数f（x）在区间[0，m]上恰好有10个零点，求正数m的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）．
    （1）若x∈[2，6]时，f（x）max=f（2）=2，f（x）min=f（6）=-2且f（x）在[2，6]上单调递减，求ω，φ的值；
    （2）若φ=$\frac{π}{6}$且函数f（x）在[0，$\frac{π}{3}$]上单调递增，求ω的取值范围；
    （3）若φ=0且函数f（x）=0在[-π，π]上恰有19个根，求ω的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知集合M={1，2}，N={|m|}．下面甲、乙、丙、丁四位同学给出四种说法：
    甲：若m=1，则N⊆M；乙：若N⊆M，则m=1；
    丙：则若m≠1，N?M；丁：m=1和N⊆M成立没有关系．
    你认为哪位同学的说法正确？

    查看答案和解析>>

    同步练习册答案