
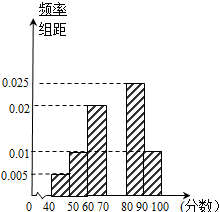
 某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.分析 (1)根据图中所有小长方形的面积之和等于1,即可求出成绩落在[70,80)上的频率;
(2)根据中位数的定义即可求出;
(3)求出成绩不低于60的频率,再估计该校高一年级期中考试物理成绩不低于60分的人数.
解答 解:(1)由于图中所有小长方形的面积之和等于1,所以成绩落在[70,80)上的频率p=1-10×(0.005+0.01+0.02+0.025+0.01)=0.3,
所以[70,80)的小长方形高为0.03,如图,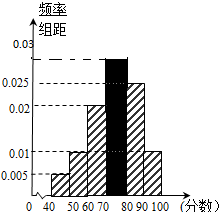
(2)由图估计40名学生物理成绩的中位数为$80-\frac{(0.005+0.01+0.02+0.03)×10-0.5}{0.03}=75$分,
(3)根据频率分布直方图,成绩不低于60的频率为1-10(0.005+0.01)=0.85.
由于该校高一年级共有学生840人,利用样本估计总体的思想,可估计该校高一年级数学成绩不低于60分的人数约为840×0.85=714人.
点评 本题主要考查频率分步直方图,中位数,属于基础题.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | |||
| “不认可”手机 | |||
| 合计 |
| P(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 焦点在y轴上的双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
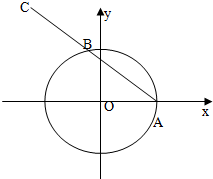 如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.
如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 |
| 广州 | 118 | 东莞 | 137 | 中山 | 95 | 江门 | 78 | 云浮 | 76 | 茂名 | 107 | 揭阳 | 80 |
| 深圳 | 94 | 珠海 | 95 | 湛江 | 75 | 潮州 | 94 | 河源 | 124 | 肇 庆 | 48 | 清远 | 47 |
| 佛山 | 160 | 惠州 | 113 | 汕头 | 88 | 汕尾 | 74 | 阳江 | 112 | 韶关 | 68 | 梅州 | 84 |
| 空气质量 | 优质 | 良好 | 轻度污染 | 中度污染 |
| AQI值范围 | [0,50) | [50,100) | [100,150) | [150,200) |
| 城市个数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com