
分析 (1)利用数量积的坐标运算得答f(x),然后利用降幂公式和辅助角公式化简,再由复合函数的单调性求得函数的单调增区间;
(2)由已知x的范围求得函数的最小值,得到m值,再由函数图象的平移得答案.
解答 解:(1)∵(2cosx,$\sqrt{3}$sinx),$\overrightarrow b$=(cosx,2cosx),
∴f(x)=$\overrightarrow a$•$\overrightarrow b$+m=$2co{s}^{2}x+2\sqrt{3}sinxcosx+m$
=$\sqrt{3}sin2x+cos2x+m+1$=$2sin(2x+\frac{π}{6})+m+1$.
由$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$,
得$-\frac{π}{3}+kπ≤x≤\frac{π}{6}+kπ,k∈Z$.
∴f(x)的单调递增区间[$kπ-\frac{π}{3},kπ+\frac{π}{6}$](k∈Z);
(2)当x∈[0,$\frac{π}{2}}$]时,$2x+\frac{π}{6}∈$[$\frac{π}{6},\frac{7π}{6}$],
∴2sin(2x$+\frac{π}{6}$)∈[-1,2],则f(x)min=m=2,
∴f(x)=$2sin(2x+\frac{π}{6})+3$,
将函数y=f(x)的图象上的点纵坐标不变,横坐标缩小到原来的$\frac{1}{2}$,
所得函数解析式为y=2sin(4x+$\frac{π}{6}$)+3,
再把所得的图象向右平移$\frac{π}{12}$个单位,得到函数y=g(x)的图象,
则g(x)=2sin[4(x-$\frac{π}{12}$)+$\frac{π}{6}$]+3=2sin(4x-$\frac{π}{6}$)+3.
点评 本题考查平面向量的数量积运算,考查了y=Asin(ωx+φ)型函数的图象和性质,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
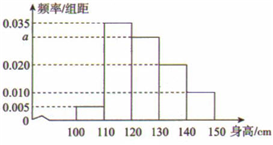 从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动.
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
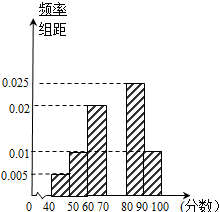 某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com