
分析 将递推式an+1=3an+3n+1+λ2n两边同除以3n+1,整理得$\frac{an+1}{3n+1}$=$\frac{an}{3n}$+1+$\frac{λ}{3}$•($\frac{2}{3}$)n,可得$\frac{an+1}{3n+1}$-($\frac{2}{3}$)n+1=$\frac{an}{3n}$+$\frac{λ-2}{3}$•($\frac{2}{3}$)n+1,利用数列{$\frac{a_n}{3^n}$-($\frac{2}{3}$)n}为等差数列,即可得出.
解答 解:将递推式an+1=3an+3n+1+λ2n两边同除以3n+1,整理得$\frac{an+1}{3n+1}$=$\frac{an}{3n}$+1+$\frac{λ}{3}$•($\frac{2}{3}$)n.
两边同减($\frac{2}{3}$)n+1,整理得$\frac{an+1}{3n+1}$-($\frac{2}{3}$)n+1=$\frac{an}{3n}$+$\frac{λ-2}{3}$•($\frac{2}{3}$)n+1,
由于{$\frac{an}{3n}$-($\frac{2}{3}$)n}为等差数列,∴$\frac{λ-2}{3}$=-1,解得λ=-1.
故答案为:-1.
点评 本题考查了数列的递推关系、等差数列的定义,考查了转化能力与计算能力,属于中档题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | |||
| “不认可”手机 | |||
| 合计 |
| P(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
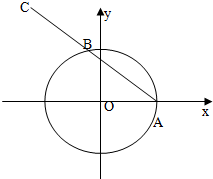 如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.
如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com