
分析 (1)三种方法:法一:直接利用组合数的计算公式即可证明.
法二:(构造)从一个装有n个不同的红球和1个黄球的口袋中取出m个不同球,共得到$C_{n+1}^m$个不同组合,我们可将这些组合分成两类:一类全是红球,则从n个红球中取m个不同的球;一类含有黄球,则从n个红球中再取出m-1个,即可得出.
法三(构造)分别求(1+x)n+1和(1+x)(1+x)n的展开式中xm的系数,利用二项式定理的展开式即可得出.
(2)法一:倒序相加法;
法二:公式法:利用公式$rC_n^r=nC_{n-1}^{r-1}$和$C_n^0+C_n^1+…+C_n^n={2^n}$,即可证明.
法三:构造函数f (x)=(1+x)n=$C_n^0+C_n^1x+C_n^2{x^2}+…+C_n^nx_{\;}^n$,两边求导得:令x=1即可证明.
解答 证明:(1)三种方法:法一:直接代公式:Cnm+Cnm-1=$\frac{n!}{m!(n-m)!}$+$\frac{n!}{(m-1)!(n-m+1)!}$=$\frac{n!(n-m+1)}{m!(n-m+1)!}$+$\frac{n!m}{m!(n-m+1)!}$=$\frac{(n+1)•n!}{m!(n-m+1)!}$=$\frac{(n+1)!}{m!(n+1-m)!}$,
又Cn+1m=$\frac{(n+1)!}{m!(n+1-m)!}$,∴Cnm+Cnm-1=Cn+1m.
法二:(构造)从一个装有n个不同的红球和1个黄球的口袋中取出m个不同球,共得到$C_{n+1}^m$个不同组合,我们可将这些组合分成两类:一类全是红球,则从n个红球中取,可得到$C_n^m$个不同组合;一类含有黄球,则从n个红球中再取出m-1个,则得到$C_n^{m-1}$个不同组合,所以$C_n^m+C_n^{m-1}=C_{n+1}^m$.
法三(构造)分别求(1+x)n+1和(1+x)(1+x)n的展开式中xm的系数,
(1+x)n+1的展开式中xm的系数为$C_{n+1}^m$;
(1+x)(1+x)n=(1+x)($C_n^0+C_n^1x+…+C_n^{m-1}x_{\;}^{m-1}+C_n^m{x^m}+…+C_n^nx_{\;}^n$)的展开式中xm的系数为1×$C_n^m$+1×$C_n^{m-1}$=$C_n^m$+$C_n^{m-1}$,
∵(1+x)n+1=(1+x)(1+x)n,∴展开式中xm的系数也相等,∴$C_n^m+C_n^{m-1}=C_{n+1}^m$.
(2)法一:倒序相加法:f(n)=Cn1+2Cn2+3Cn3+…+nCnn,f(n)=nCnn+(n-1)${∁}_{n}^{n-1}$…+3Cn3+2Cn2+Cn1,∴2f(n)=nCnn+(n-1+1)${∁}_{n}^{1}$+…+(1+n-1)${∁}_{n}^{n-1}$+n${∁}_{n}^{n}$
=n(${∁}_{n}^{0}$+${∁}_{n}^{1}$+…+${∁}_{n}^{n-1}$+${∁}_{n}^{n}$)=n•2n,∴f(n)=n•2n-1.
法二:公式法:利用公式$rC_n^r=nC_{n-1}^{r-1}$,则Cn1+2Cn2+3Cn3+…+nCnn=n${∁}_{n-1}^{0}$+n${∁}_{n-1}^{1}$+…+n${∁}_{n-1}^{n-1}$=n(${∁}_{n-1}^{0}$+${∁}_{n-1}^{1}$+…+${∁}_{n-1}^{n-1}$)=n•2n-1,
∴Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1.
法三:构造函数f (x)=(1+x)n=$C_n^0+C_n^1x+C_n^2{x^2}+…+C_n^nx_{\;}^n$,两边求导得:$n{(1+x)^{n-1}}=C_n^1+2C_n^2{x^1}+3C_n^3{x^2}…+nC_n^nx_{\;}^{n-1}$
令x=1得:$C_n^1+2C_n^2+3C_n^3+…+nC_n^n=n•{2^{n-1}}$成立.
点评 本题考查了二项式定理展开式的系数的性质、组合数的性质、组合数的计算公式、“倒叙相加法”、“构造法”、“导数法”,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
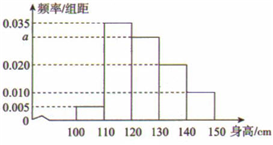 从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动.
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
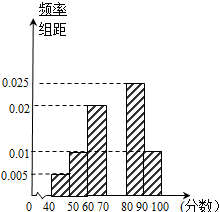 某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期末考试物理成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com