
| A. | (5,8) | B. | (8,9) | C. | (5,9) | D. | (8,+∞) |
分析 根据f(x)的性质可得ln(a-1)+ln(b-1)=0,从而得出a,b的关系,从而得出得出-a+5b关于b(或者a)的函数,求出此函数的值域即可.
解答 解:f(x)=|ln(x-1)|=$\left\{\begin{array}{l}{-ln(x-1),1<x≤2}\\{ln(x-1),x>2}\end{array}\right.$,
∴f(x)在(1,2)上单调递减,在(2,+∞)上单调递增,
∵f(a)=f(b),a<b,
∴ln(a-1)+ln(b-1)=0,即ln[(a-1)(b-1)]=0,且1<a<2,b>2.
∴(a-1)(b-1)=1.
∴a=$\frac{1}{b-1}+1$=$\frac{b}{b-1}$.
∴-a+5b=$\frac{-b}{b-1}$+5b=$\frac{5{b}^{2}-6b}{b-1}$=$\frac{5(b-1)^{2}+4(b-1)-1}{b-1}$=5(b-1)-$\frac{1}{b-1}$+4,
令b-1=t,g(t)=5t-$\frac{1}{t}$+4,则g(t)在(2,+∞)上是增函数,且g(2)=8,
∴g(t)的值域为(8,+∞).
∴-a+5b的范围是(8,+∞).
故选:D.
点评 本题考查了函数的单调性与最值,对数函数的性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | |||
| “不认可”手机 | |||
| 合计 |
| P(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
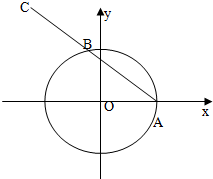 如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.
如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
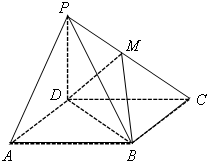 如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 |
| 广州 | 118 | 东莞 | 137 | 中山 | 95 | 江门 | 78 | 云浮 | 76 | 茂名 | 107 | 揭阳 | 80 |
| 深圳 | 94 | 珠海 | 95 | 湛江 | 75 | 潮州 | 94 | 河源 | 124 | 肇 庆 | 48 | 清远 | 47 |
| 佛山 | 160 | 惠州 | 113 | 汕头 | 88 | 汕尾 | 74 | 阳江 | 112 | 韶关 | 68 | 梅州 | 84 |
| 空气质量 | 优质 | 良好 | 轻度污染 | 中度污染 |
| AQI值范围 | [0,50) | [50,100) | [100,150) | [150,200) |
| 城市个数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 两条射线 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com