
分析 (1)讨论x的范围:x≤-$\frac{1}{2}$,-$\frac{1}{2}$<x≤1,x≥1,去掉绝对值,写出分段函数的形式,画出图象;
(2)通过图象可得最大值m,设a2+b2+2c2=a2+tb2+(1-t)b2+2c2≥2$\sqrt{t}$ab+2$\sqrt{2(1-t)}$bc,令2$\sqrt{t}$:2$\sqrt{2(1-t)}$=1:2,求出t的值,即可得到所求最大值.
解答 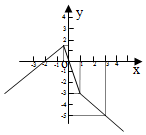 解:(1)f(x)=|x-1|-|2x+1|=$\left\{\begin{array}{l}{1-x+2x+1=x+2,x≤-\frac{1}{2}}\\{1-x-2x-1=-3x,-\frac{1}{2}<x≤1}\\{x-1-2x-1=-x-2,x>1}\end{array}\right.$,
解:(1)f(x)=|x-1|-|2x+1|=$\left\{\begin{array}{l}{1-x+2x+1=x+2,x≤-\frac{1}{2}}\\{1-x-2x-1=-3x,-\frac{1}{2}<x≤1}\\{x-1-2x-1=-x-2,x>1}\end{array}\right.$,
由分段函数的图象画法可得图象如右;
(2)由(1)知,当x=-$\frac{1}{2}$时,f(x)的最大值为$\frac{3}{2}$,即m=$\frac{3}{2}$;
∴a2+b2+2c2=$\frac{3}{2}$,
设a2+b2+2c2=a2+tb2+(1-t)b2+2c2≥2$\sqrt{t}$ab+2$\sqrt{2(1-t)}$bc,
令2$\sqrt{t}$:2$\sqrt{2(1-t)}$=1:2,即8(1-t)=16t 得:t=$\frac{1}{3}$,
∴a2+b2+2c2=a2+$\frac{1}{3}$b2+$\frac{2}{3}$b2+2c2≥2•$\frac{\sqrt{3}}{3}$ab+4•$\frac{\sqrt{3}}{3}$bc=$\frac{2\sqrt{3}}{3}$ (ab+2bc)
∴ab+2bc≤$\frac{\sqrt{3}}{2}$(a2+b2+2c2)=$\frac{3\sqrt{3}}{4}$(当且仅当a2=c2=$\frac{1}{4}$,b2=$\frac{3}{4}$时取“=”号).
点评 本题考查分段函数的图象和性质,考查最值的求法,注意运用图象和基本不等式,考查变形和化简整理的运算能力,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
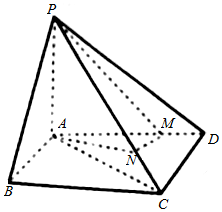 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1,2} | B. | {-1,2} | C. | {1,2} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
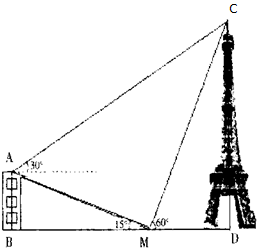 如图,一栋建筑物AB高(30-10$\sqrt{3}$)m,在该建筑 物的正东方向有一个通信塔CD.在它们之间的地面M点(B、M、D三点共线)测得对楼顶A、塔顶C的仰角分别是15°和60°,在楼顶A处 测得对塔顶C的仰角为30°,则通信塔CD的高为60m.
如图,一栋建筑物AB高(30-10$\sqrt{3}$)m,在该建筑 物的正东方向有一个通信塔CD.在它们之间的地面M点(B、M、D三点共线)测得对楼顶A、塔顶C的仰角分别是15°和60°,在楼顶A处 测得对塔顶C的仰角为30°,则通信塔CD的高为60m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{1}{2},\frac{1}{2}]$ | B. | [-2,2] | C. | (-∞,-2]∪[2,+∞) | D. | $(-∞,-\frac{1}{2}]∪[\frac{1}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com