
分析 (1)由题意将点的坐标代入解析式求出a;
(2)通过数据线的面积,三角形是锐角三角形,利用余弦定理化简求出c的范围,然后之后转化求解向量的数量积的范围.
解答 解:(1)由题意得f(x)=(asinx-cosx)cosx$+\frac{1}{2}$=$\frac{a}{2}$sin2x-$\frac{1}{2}$cos2x
∵f(x)关于点($\frac{π}{12}$,0)对称,所以f($\frac{π}{12}$)=$\frac{a}{2}$sin$\frac{π}{6}$$-\frac{1}{2}$cos$\frac{π}{6}$=0;
解得a=$\sqrt{3}$.
(2)由(1)可知f(x)=sin(2x-$\frac{π}{6}$).锐角三角形ABC的三内角A,B,C所对的边分别为a,b,c,若f(A)=1,可得:sin(2x-$\frac{π}{6}$)=1,解得A=$\frac{π}{3}$,△ABC的面积为$\frac{\sqrt{3}}{4}$,$\frac{1}{2}bcsinA=\frac{\sqrt{3}}{4}$,所以bc=1,
$\overrightarrow{BA}$•$\overrightarrow{BC}$=accosB=ac×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2}$=$\frac{{b}^{2}+{c}^{2}-2bccosA+{c}^{2}-{b}^{2}}{2}$=c2-$\frac{1}{2}$.
因为△ABC为锐角三角形,所以$\left\{\begin{array}{l}{{a}^{2}+{c}^{2}>{b}^{2}}\\{{a}^{2}+{b}^{2}>{c}^{2}}\end{array}\right.$,又a2=b2+c2-1,所以$\left\{\begin{array}{l}{{b}^{2}>\frac{1}{2}}\\{{c}^{2}>\frac{1}{2}}\end{array}\right.$,
又bc=1,所以$\frac{1}{2}$<c2<2,
故$\overrightarrow{BA}$•$\overrightarrow{BC}$的取值范围是(0,$\frac{3}{2}$).
点评 本题主要考查了三角函数恒等变化的应用,考查了正弦定理,余弦定理,向量的数量积的运算等知识的综合应用,考查了正弦函数的图象和性质,综合性强,考查了三角函数的化简以及利用正弦函数的性质求sin(2x-$\frac{π}{6}$)的最值.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(理)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图,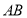 是
是 的直径,
的直径,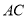 是
是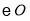 的切线,
的切线, 交
交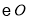 于点
于点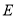 .
.
(1)过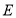 做
做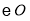 的切线,交
的切线,交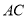 与点
与点 ,证明:
,证明: 是
是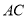 的中点;
的中点;
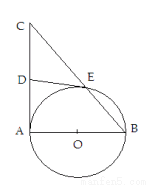
(2)若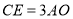 ,求
,求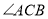 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com