
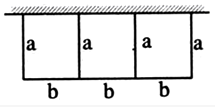
分析 设出宽,进而可表示出长,利用矩形面积公式求得面积的表达式,再利用二次函数的性质求得矩形面积的最大值.
解答 解:设每个小矩形的高为am,则长为b=$\frac{1}{3}$(100-4a)m,记面积为Sm2
则S=3ab=a•(100-4a)=-4a2+100a=-4(a-$\frac{25}{2}$)2+625(0<a<25)
∴当a=12.5时,Smax=625(m2)
∴所围矩形面积的最大值为625m2
故答案为625.
点评 本题以实际问题为载体,考查了函数的最值在实际中的应用.考查了学生运用所学知识解决实际问题的能力,设出自变量和因变量,将实际问题转化为函数模型是解答本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | ±3 | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
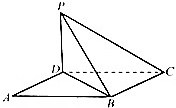 如图,在平行四边形ABCD中,BD=4$\sqrt{3}$,PD⊥平面ABCD,平面PBC⊥平面PBD,二面角P-BC-D为60°
如图,在平行四边形ABCD中,BD=4$\sqrt{3}$,PD⊥平面ABCD,平面PBC⊥平面PBD,二面角P-BC-D为60°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
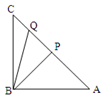 如图,在等腰直角△ABC,∠ABC=90°,AB=2$\sqrt{2}$,点P在线段AC上,若点Q在线段PC上,且∠PBQ=30°,则△BPQ的面积的最小值为8-4$\sqrt{3}$.
如图,在等腰直角△ABC,∠ABC=90°,AB=2$\sqrt{2}$,点P在线段AC上,若点Q在线段PC上,且∠PBQ=30°,则△BPQ的面积的最小值为8-4$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
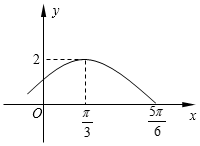 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.则A+ω+φ=3+$\frac{π}{6}$.
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.则A+ω+φ=3+$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
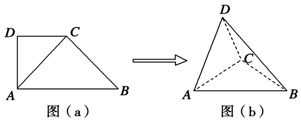 如图(a),在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=8,AD=CD=4,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图(b)所示.
如图(a),在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=8,AD=CD=4,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图(b)所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com