
分析 (1)利用零点分段法,可将函数解析式化为分段函数,进而结合一次函数的图象和性质,得到函数的图象;
(2)数形结合,可得函数的值域、单调区间;
(3)若对任意x∈R,不等式|2x-1|≥a+x恒成立,则a≤|2x-1|-x的最小值.
解答 解:(1)∵函数f(x)=|2x-1|-x=$\left\{\begin{array}{l}-3x+1,x<\frac{1}{2}\\ x-1,x≥\frac{1}{2}\end{array}\right.$,
函数的图象如下图所示: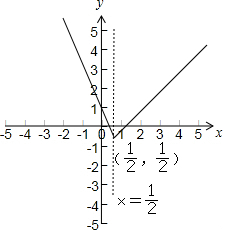
(2)由图可得:函数的值域为:[-$\frac{1}{2}$,+∞);
单调减区间为:为:(-∞,$\frac{1}{2}$],单调增区间为:[$\frac{1}{2}$,+∞);
(3)若对任意x∈R,不等式|2x-1|≥a+x恒成立,
则a≤|2x-1|-x恒成立,
即a≤-$\frac{1}{2}$.
点评 本题考查的知识点是分段函数的应用,函数的图象,函数的单调性,函数的值域,函数恒成立问题,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 12 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4032}{2016}$ | B. | $\frac{4034}{2017}$ | C. | $\frac{4032}{2018}$ | D. | $\frac{4034}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
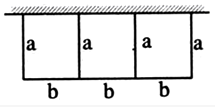
 用小正方体搭一个几何体,使得它的正视图和俯视图如图所示,这样的几何体只有一种吗?若不是,则这种几何体最少需要多少个小正方体?最多需要多少个小正方体?
用小正方体搭一个几何体,使得它的正视图和俯视图如图所示,这样的几何体只有一种吗?若不是,则这种几何体最少需要多少个小正方体?最多需要多少个小正方体?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (1,+∞) | C. | (3,+∞) | D. | [-$\frac{9}{4}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com