
| A. | (-∞,0)∪(0,1) | B. | (0,+∞) | C. | (-1,0)∪(0,3) | D. | (-∞,1) |
分析 令F(x)=f(x)+2x,求出导函数F'(x)=f'(x)+2>0,判断F(x)在定义域内单调递增,由f(1)=1,转化$f({log_2}|{3^x}-1|)<3-{log_{\sqrt{2}}}|{3^x}-1|$为$f({log_2}|{3^x}-1|)+2{log_2}|{3^x}-1|<3$,然后求解不等式即可.
解答 解:令F(x)=f(x)+2x,有F'(x)=f'(x)+2>0,
所以F(x)在定义域内单调递增,由f(1)=1,得F(1)=f(1)+2=3,因为$f({log_2}|{3^x}-1|)<3-{log_{\sqrt{2}}}|{3^x}-1|$等价于$f({log_2}|{3^x}-1|)+2{log_2}|{3^x}-1|<3$,
令$t={log_2}|{3^x}-1|$,有f(t)+2t<3,则有t<1,即${log_2}|{3^x}-1|<1$,
从而|3x-1|<2,解得x<1,且x≠0.
故选:A.
点评 本题是考查导数在研究函数单调性上的应用.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -4 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 堑堵,我国古代数学名词,其三视图如图所示.《九章算术》中有如下问题:“今有堑堵,下广二丈,袤一十八丈六尺,高二丈五尺,问积几何?”意思是说:“今有堑堵,底面宽为2丈,长为18丈6尺,高为2丈5尺,问它的体积是多少?”(注:一丈=十尺).答案是( )
堑堵,我国古代数学名词,其三视图如图所示.《九章算术》中有如下问题:“今有堑堵,下广二丈,袤一十八丈六尺,高二丈五尺,问积几何?”意思是说:“今有堑堵,底面宽为2丈,长为18丈6尺,高为2丈5尺,问它的体积是多少?”(注:一丈=十尺).答案是( )| A. | 25500立方尺 | B. | 34300立方尺 | C. | 46500立方尺 | D. | 48100立方尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
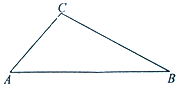 如图,已知△ABC中,角A,B,C的对边分别为a,b,c,C=120°.
如图,已知△ABC中,角A,B,C的对边分别为a,b,c,C=120°.查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:填空题
下列各小题中, 是
是 的充分必要条件的是___________.
的充分必要条件的是___________.
① 或
或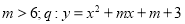 有两个不同的零点;
有两个不同的零点;
②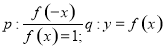 是偶函数;
是偶函数;
③ ;
;
④ ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com