【题目】如图，几何体ABCDE中，△ABC是正三角形，EA和DC都垂直于平面ABC，且EA=AB=2a，DC=a，F，G分别为EB和AB的中点．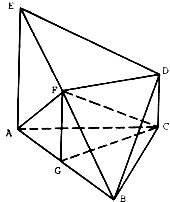 
（1）求证：FD∥平面ABC；
（2）求二面角B﹣FC﹣G的正切值．
【答案】
（1）证明：连CG，FG，则四边形DEGC是平行四边形，得到DF∥CG
DF平面ABC，CG平面ABC
所以FD∥平面ABC
（2）证明：设二面角B﹣FC﹣G的大小为α
易知BG⊥平面FCG，所以△FCG为△BFC的射影
∴cosα= 
∴tanα= 
【解析】（1）连CG，FG，由已知中F是BE的中点，结合三角形中位线的性质，可得FG平行且等于AE的一半，又由EA、CD都垂直于平面ABC，且EA=2a，DC=a，可得四边形DEGC是平行四边形，进而得到DF∥CG，由线面平行的判定定理即可得到FD∥平面ABC；（2）易知BG⊥平面FCG，所以△FCG为△BFC的射影，故分别计算面积可求二面角的余弦值，从而得解．
科目：高中数学 来源： 题型：
【题目】已知椭圆的中心在原点，焦点为
，且离心率为 
.
（1）求椭圆的方程；
（2）直线（与坐标轴 不平行）与椭圆交于不同的两点，且线段中点的横坐标为
，求直线倾斜角的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知△ABC的三个内角分别为A，B，C，且A≠ 
．
（1）化简 
；
（2）若角A满足sinA+cosA= 
．
（i）试判断△ABC是锐角三角形还是钝角三角形，并说明理由；
（ii）求tanA的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司准备将1000万元资金投入到市环保工程建设中，现有甲、乙两个建设项目选择，若投资甲项目一年后可获得的利润
（万元）的概率分布列如下表所示：
且
的期望
；若投资乙项目一年后可获得的利润
（万元）与该项目建设材料的成本有关，在生产的过程中，公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整，两次调整相互独立且调整的概率分别为
和
.若乙项目产品价格一年内调整次数
（次数）与
的关系如下表所示：
（1）求
的值；
（2）求
的分布列；
（3）若
，则选择投资乙项目，求此时
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如表资料：
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻两个月的概率；
(2)若选取的是1月与6月的两组数据，请根据3至5月份的数据，求出
关于
的线性回归方程
；
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问（2）中所得线性回归方程是否理想？
参考公式：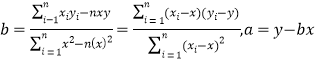
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某超市连锁店统计了城市甲、乙的各16台自动售货机在中午12：00至13：00间的销售金额，并用茎叶图表示如图．则有（ ）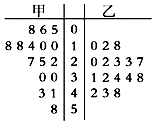 
A.甲城销售额多，乙城不够稳定
B.甲城销售额多，乙城稳定
C.乙城销售额多，甲城稳定
D.乙城销售额多，甲城不够稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
